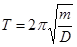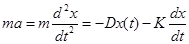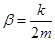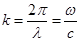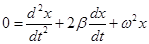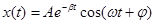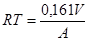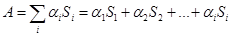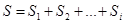Eine Schwingung mit konstanter Amplitude heißt ungedämpft. Nimmt die Amplitude mit der Zeit ab, so handelt es sich um eine gedämpfte Schwingung. Schallwellen sind mechanische Wellen, zu deren Fortpflanzung ein Medium benötigt wird. Hier pflanzt sich der Bewegungszustand fort und nicht das Material selbst ("Energietransport ohne Stofftransport").

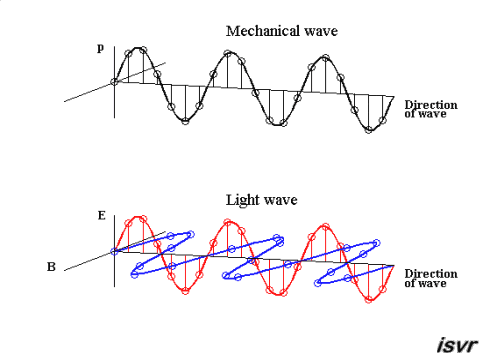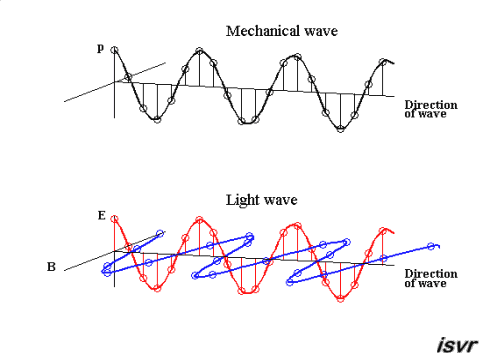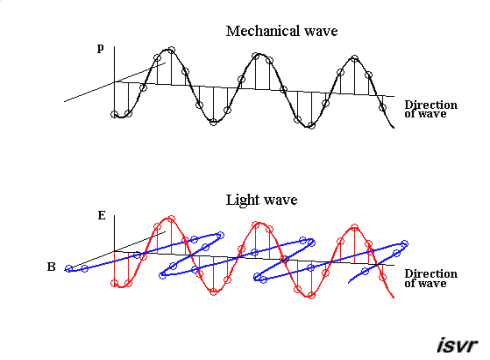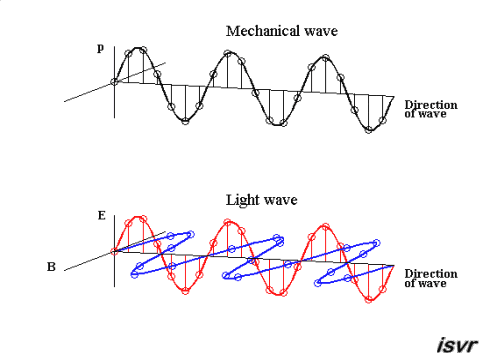
Abbildung. Darstellung von einer mechanischen und elektromagnetischen Welle.

[http://ffden-2.phys.uaf.edu/631fall2008_web.dir/wallace_webpage/4_Elec.html]

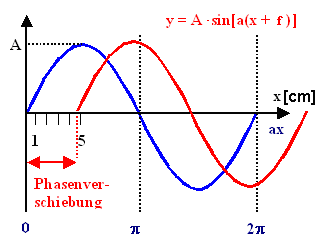
Abbildung. Darstellung der Wellenausbreitung.

[http://www.acs.psu.edu/drussell/demos.html]

1.2 Die harmonische Schwingung

Jeder Schall kann in Zusammensetzung von Sinus-Grundschwingungen aufgeteilt werden (Fourier). Der wichtigste Schwingungstyp ist die harmonische Schwingung (Sinusschwingung):

y(t) = Asin(ωt+φ)

wobei y(t) bezeichnet den Momentanwert der Auslenkung, A ist Amplitude, ω ist die Kreisfrequenz in [rad/sec] und ω = 2πf.

Abbildung. Phasenverschiebung.

[http://www.tf.uni-kiel.de/matwis/amat/mw2_ge/kap_3/basics/t3_4_1.html]

Die folgende Abbildung zeigt die komplexe Beschreibung von Sinuswellen.

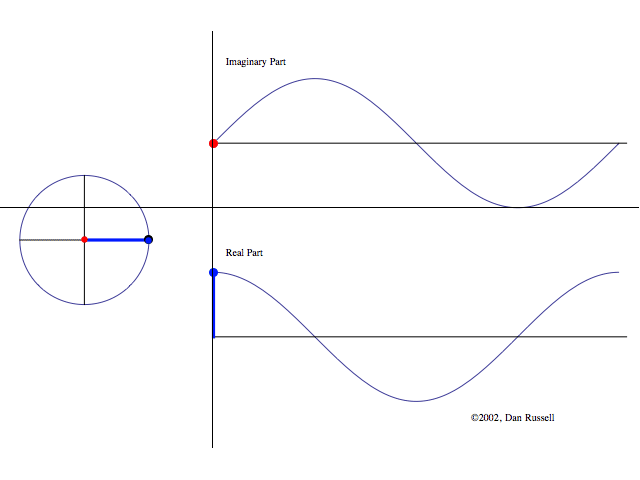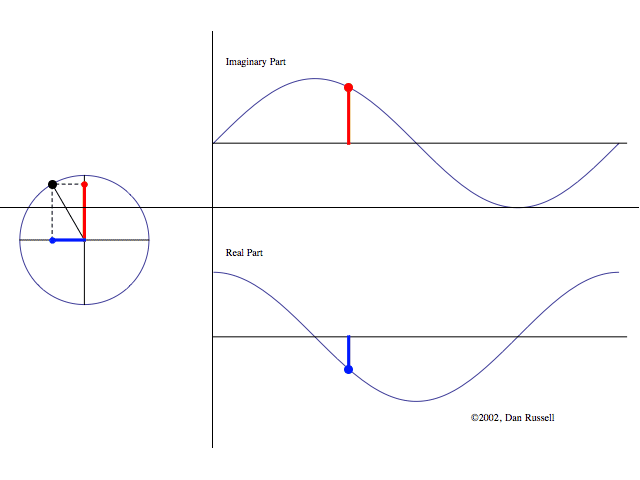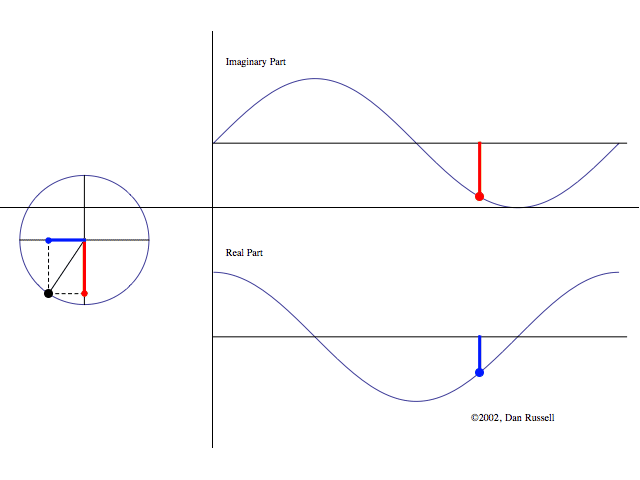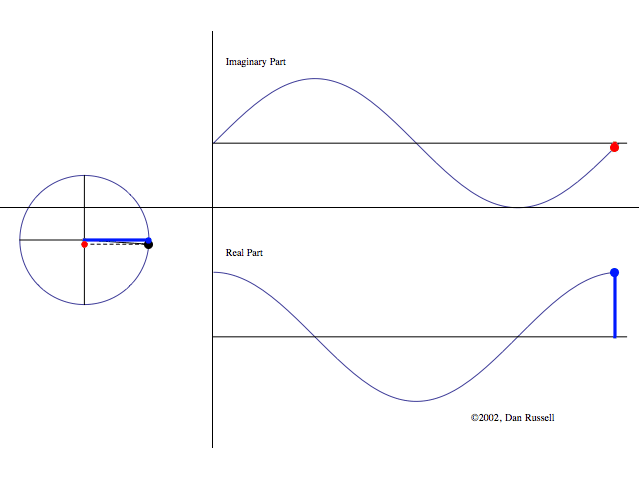
Abbildung. Darstellung eines "sweep sinus" Tons. Es besteht aus reiner Sinuswellen von 20 Hz bis 20 kHz. Sie werden nach einander innerhalb von 10 Sekunden abgespielt. Klicken Sie auf das Bild für die Wiedergabe.

[http://www.tf.uni-kiel.de/matwis/amat/mw2_ge/kap_3/basics/t3_4_1.html]

1.3 Grundeinheiten

Die folgende Tabelle zeigt die wichtigsten Grundeinheiten und deren Zusammenhang.

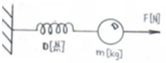
1.4 Pendelgleichung

Eine homogene, lineare Differentialgleichung 2. Ordnung mit konstanten Koeffizienten:

x'' + kx = 0

ist in der Physik als Pendelgleichung bekannt. Bei ungedämpfter Schwingung:

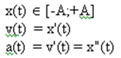
Die Gleichung kann wie folgend abgeleitet werden:

F = F _feder+F_brems+F_extern = ma

a(t) = d²x(t)/dt²

F_feder = -Dx(t)

F_brems = F_reib = -konst*v(t)

F_extern = z.B. Schwerkraft.

F = ma = -Dx

Die Lösung dieser Differentialgleichung ist: x(t) = C₁sin(ωt)+C₂cos(ωt)

Frequenz der Bewegung ist: f=1/T, wobei

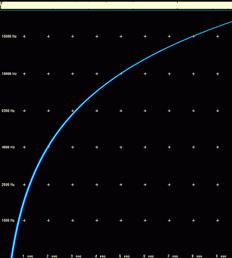
Bei gedämpfter Schwingung sieht die Gleichung wie folgend aus:

Wobei Dämpfungsfaktor und Wellenzahl sind:

und die Eigenfrequenz ist: ω = D/m = 2πf. Die Schwingung wird exponentiell gedämpft:

Die Lösung dieser Differentialgleichung - wenn Bremskraft klein - ist:

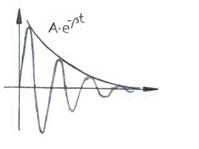
Abbildung. Lösung bei gedämpfter Schwingung.

Wenn Bremskraft groß ist, kann keine periodische Schwingung bilden. Schauen Sie sich das folgende Video an. http://www.youtube.com/watch?v=eyO1UlrPqIQ

Der Zusammenhang zwischen Wellenlänge und Frequenz ist:

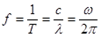
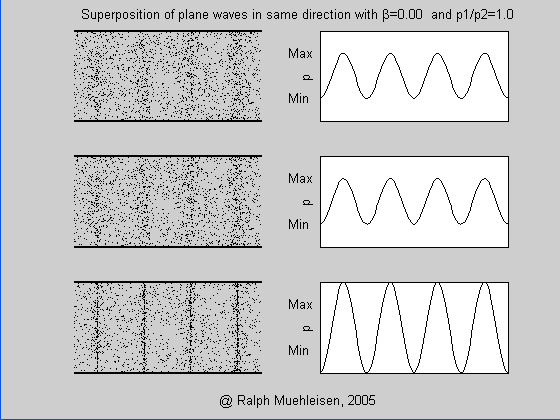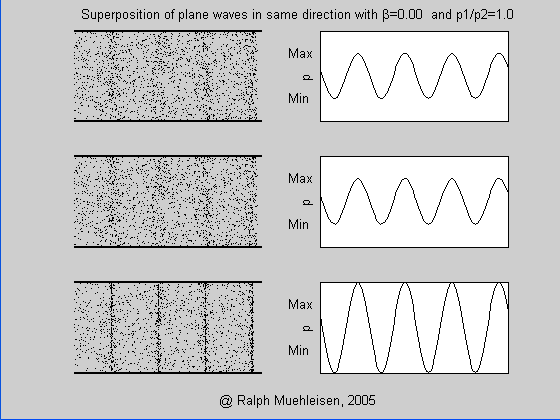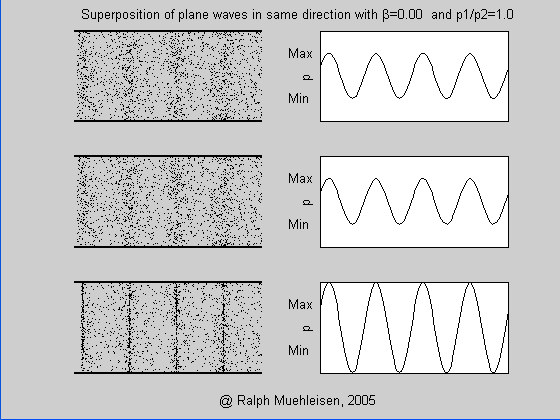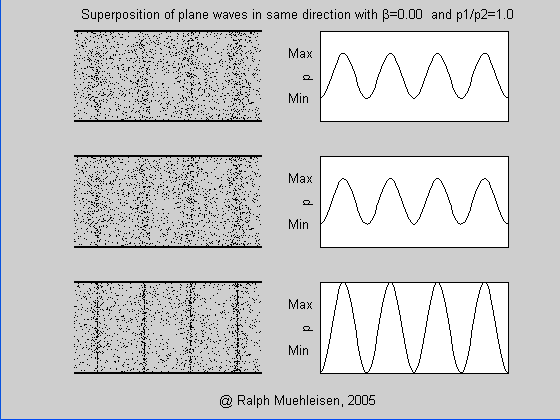
Abbildung. Wellen mit verschiedener Amplitude.

[http://ralphmuehleisen.com/animations.html]

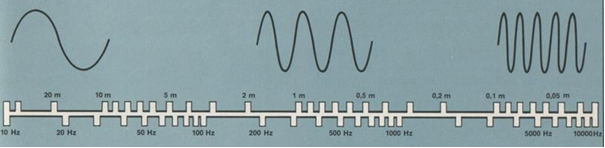
Abbildung. Zusammenhang zwischen Wellenlänge und Frequenz in der Luft.

[http://www.bksv.com/]

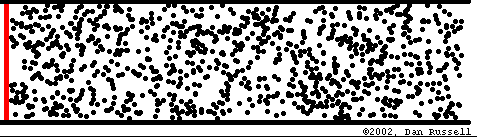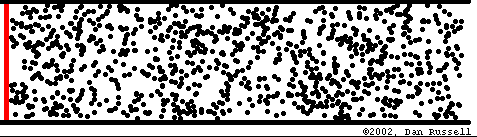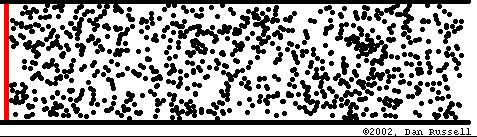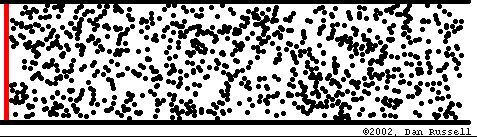
Abbildung. Ausbreitung eines Impulses.

[http://www.acs.psu.edu/drussell/demos.html]

Abbildung. Bewegung bei einer transversalen Welle.

[http://www.acs.psu.edu/drussell/demos.html]

1.5 Schallgeschwindigkeit

Schallgeschwindigkeit in der Luft beträgt 328-344 m/s. Bei +1 Celsius wird es um +0,6 m/s grösser. Die Schallgeschwindigkeit ist in - akustisch gesehen - dichteren Materialien wie Flüssigkeiten und festen Körpern größer. Die Ursache ist die stärkere Bindung unter den Teilchen, so ist die Energieübergabe zwischen den Molekülen schneller. z.B. die Schallgeschwindigkeit im Wasser beträgt 1400 m/s, im Stahl ca. 5000 m/s. Selbe Frequenz und ein anderes Medium bedeutet andere Wellenlänge! Ein Kundtsches Rohr kann die Wellenausbreitung anzeigen und sogar ist es möglich mit ihm die Schallgeschwindigkeit zu messen: http://www.youtube.com/watch?v=N8q4xAL2WpU

1.6 Schalldruck und Schallintensität

Der wichtigste Parameter von Schallwellen, der durch die Ohren und auch durch Mikrofone wahrgenommen wird, ist der Schalldruck. Es ist der sich zeitlich ändernde Anteil des Luftdrucks in N/m², d.h. Pascal. Da Druck mit keiner Richtungsangabe verknüpft werden kann, handelt es sich um eine skalare Größe. (f ist die Kraft, A ist die Fläche, worauf die Kraft wirkt): p=f/A [Pa]. Schalldruck ist ein Parameter des Schallfeldes und nicht der Schallquelle.

Der andere wichtige Parameter von Schallwellen ist die Intensität. Es beschreibt den Energiefluss, d.h. die Energie, die pro Zeiteinheit (Sekunde) eine senkrecht zur Abstrahlrichtung stehende Einheitsfläche passiert. Es ist die Energie, die eine 1 m2 Fläche in 1 s passiert. Mit dem Schalldruck p und der Teilchengeschwindigkeit v ist:

i = pv [W/m²].

Schallintensität ist eine vektorielle Größe mit Richtung. Die Größen Schalldruck und Schallintensität werden in der Regel als Pegel (in dB=Dezibel) angegeben. Unter dem Begriff "Pegel" wird das logarithmierte Verhältnis von gemessenem Wert zu einem genormten Bezugswert verstanden.

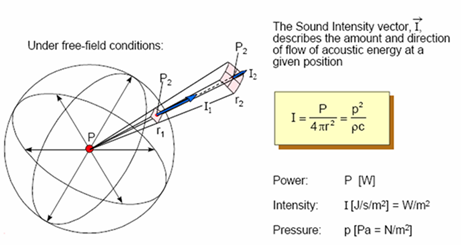
Abbildung. Interpretation von Schalldruck und Schallintensität.

[http://www.bksv.com/]

1.7 Pegelrechnung

Die Benutzung des Logarithmus ist in der Akustik selbstverständlich, denn

die Wahrnehmung, das Gehör arbeitet logarithmisch: das sogenannte subjektive Lautheit ist mit dem Logarithmus von den Grundeinheiten proportional,
die Grenzen von Minimal- und Maximalwerten sind sehr groß sowohl in der Frequenz als auch in der Amplitude (Gehör: 1:1000 bzw. 1:1M in der Frequenz und Amplitude)
die Berechnungen mit Addieren und Subtraktion ist einfacher, als mit Multiplikation und Teilen (z.B. bei Verstärkern).

Der Intensitätspegel ist:

I = 10 log( I/I₀ ) [dB]

wobei I₀ = 10^-12 W/m².

Der Schalldruckpegel ist:

P = 10 log (P²/p₀²) = 20 log( P/p₀) [dB]

wobei p₀= 20 µPa.

Aufgabe: Bestimmen Sie wie viel dB ist 2 Pa Schalldruck:

P = 20 log ( 2 Pa/20 µPa ) = 20 log( 2/20x10^-6) = 20 log (10⁵) = 20x5 = 100 dB.

Abbildung. Darstellung von Schallquellen und Pegelwerten.

[http://www.bksv.com/]

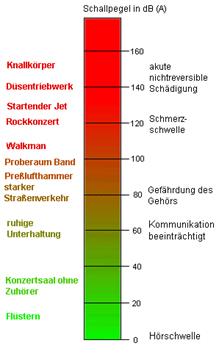
Abbildung. Darstellung von Pegelwerten in dB(A).

[http://www.dasp.uni-wuppertal.de/ars_auditus/akustik/akustik5.htm]

Im "freien Schallfeld" sinkt der Schalldruck nach dem reziproke Abstandgesetz "1/r". (-6 dB bei doppelter Entfernung)

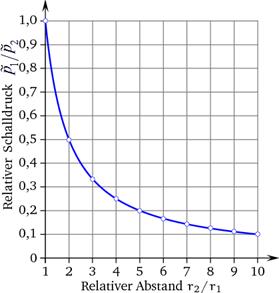
Abbildung. Abstandgesetz 1/r. [http ://www.sengpielaudio.com/Rechner-abstandsgesetz.htm ]

Addieren von dB-Werten ist schwierig. Wenn eine Schallquelle mit einer zweiten Schallquelle vom selben Schalldruckpegel ergänzt wird, ist der Pegel mit 3 dB erhöht. Die Ursache dafür ist, dass beim Addieren müssen die Logarithmen von quadratischen Größen addiert werden (wie bei Schallleistung, da es hier um die Verdopplung von der Schallenergie geht).

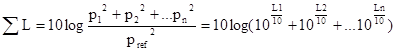
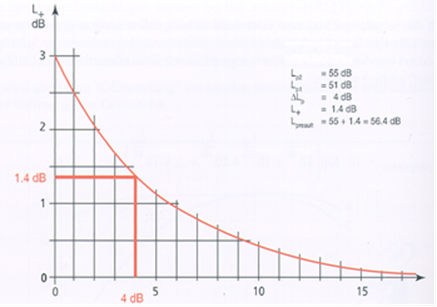
Abbildung. Hilfsdiagram für Addieren von Pegelwerten.

[http://www.bksv.com/]

*******************************************************************************************************************************************************

2. Schallausbreitung in verschiedenen Umgebungen

2.1 Quellen

Mathematische Modellbildung = Punktquelle. Eine Punktquelle ist "unendlich klein", oder im Gegensatz zur Wellenlänge sehr klein. Da Lautsprecher und andere Schallquellen mehrere Frequenzen ausstrahlen können und eine wirkliche Größe haben, können in der Praxis nicht als Punktquelle betrachtet werden. Selten können wir Schallquellen als Linienquelle (Straße, Tunnel) betrachten.

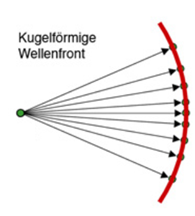
Abbildung. Kugelförmige Wellenfront.

[http://www.mpia-hd.mpg.de/~hippler/AOonline/C05/ao_online_05_01.html]

Die zwei wichtigsten Wellen sind Kugelwellen und ebene Wellen. Bei Ebene Welle sind Wellenfronten Ebenen senkrecht zur Ausbreitungsrichtung. Bei Kugelwelle sind Wellenfronten Oberflächen konzentrischer Kugeln um die Quelle. Selten kommen auch Zylinderwellen vor.

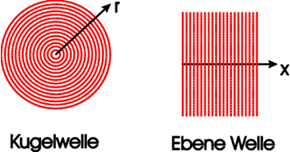
Abbildung. Kugelwelle und ebene Welle.

[http://mv-sirius.fh-offenburg.de/Physik/wellen.htm]

In idealer Schallausbreitung entsteht eine Kugelwelle. Bei der Kugelwelle verteilt sich die Energiedichte auf immer größere Flächen, d. h. sie nimmt mit 1/r² ab. Daraus ergibt sich eine Abnahme des Schalldrucks mit 1/r. (Quadratische Energie-Abstandsgesetz).

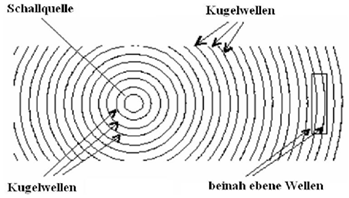
Abbildung. Kugelwellen weit von der Schallquelle können als beinah ebene Wellen angesehen werden.

[http://mv-sirius.fh-offenburg.de/Physik/wellen.htm]

Das 1/r²-Abstandsgesetz der Bestrahlungsstärke gilt in der Umgebung eines punktförmigen, isotropen Strahlers. Die Überlegungen gelten für jede beliebige Art der Strahlung, solange die Strahlung nicht absorbiert wird.
Um diese Voraussetzungen zumindest annähernd zu realisieren, muss man den Abstand r zwischen der Strahlenquelle und dem Messort viel größer wählen als die Ausdehnung der Strahlenquelle (Fernfeld).

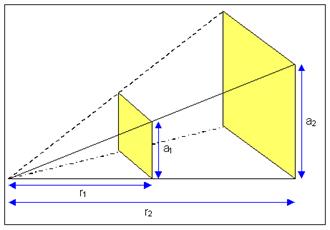
Abbildung. Darstellung von Oberflächen bei doppelter Entfernung.

[http://www.stmary.ws/highschool/physics/home/notes/electricity/staticelectricity/animations/InverseSq.html]

2.2 Freies und diffuses Schallfeld

Unter Freifeld (Direktfeld) versteht man eine Schallsituation, in der keinerlei Reflexionen auftreten. Im Freifeld wird der gesamte Schall durch den Direktschall bestimmt. Freifeldbedingungen finden sich in der Natur nur, wenn z. B. Reflexionen am Boden keine Rolle spielen. Insbesondere in der akustischen Messtechnik und bei Hörversuchen Freifeldbedingungen eine große Rolle, da dann die Ergebnisse nur von dem Schall der Schallquelle beeinflusst werden und nicht von Reflexionen des Raums. Im Freifeld ist das 1/r - Gesetz gültig. Bei der Messtechnik verwendet man spezielle Messkabinen wie schalltoter Raum und Hallraum.

Abbildung. Auto im schalltoten Raum.

[http://www.architekten24.de/]

Abbildung. Schalltoter Raum für Hörversuche in der Psychoakustik.

[http://ear.berkeley.edu/anechoic-chamber.html]

Der Abstand, bei dem Direktschall und Diffuser Schall den gleichen Pegel erreichen, wird als Hallradius bezeichnet.

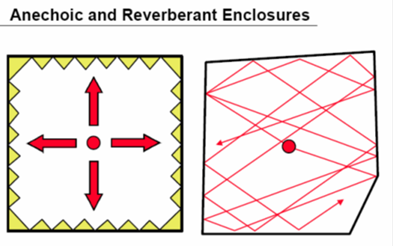
Abbildung. Schalltoter Raum (links) und Hallraum (rechts) bei einer Schallquelle.

[http://www.bksv.com/]

Abbildung. Hallraum mit reflektierenden Oberflächen für viele Reflexionen. Hier werden z.B. Absorptionskoeffizienten gemessen.

[http://w3fk05vs-n.hm.edu/fakultt/faqs_2/klima.de.html]

2.3 Wellenausbreitung mit Hindernissen

Schallwellen in der Wirklichkeit breiten sich nicht unter Freifeldbedingungen aus, sondern treffen sich mit Hindernissen. Hierzu gehört auch die Durchströmung durch Öffnungen. Die drei wichtigsten Phänomene sind:

Refraktion (a), Reflexion (b) und Diffraktion (c).

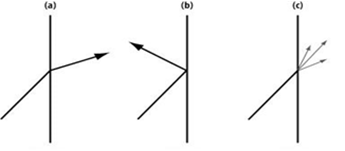
Reflexion

Die Schallreflexion ist mit der Optik vergleichbar, wenn die Abmessungen des Reflektors mindestens die fünffache Wellenlänge haben. Hierfür gilt die Regel Einfallswinkel = Reflexionswinkel auch für gekrümmte Flächen. An der Reflexionsfläche kann sich die Schallquelle spiegeln und auf der anderen Seite der Fläche abbilden. Diese neue Schallquelle wird als Spiegelschallquelle bezeichnet. Reflexionen können Echo verursachen.

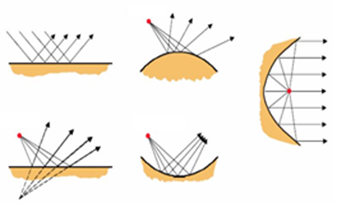
Abbildung. Varianten von Reflexionen.

[http://www.bksv.com/]

Refraktion

Die Schallbrechung, auch Refraktion, ist ein grundlegendes Phänomen. Trifft eine Schallwelle unter einem gegebenen Einfallswinkel schräg auf eine Grenzfläche auf, so wird ein gewisser Anteil in das Medium zurückgeworfen, während ein anderer Anteil in das aufnehmende Medium eindringt und sich dort weiter ausbreitet. Dabei erfährt der Schall eine Richtungsänderung.

Abbildung. Animation von Refraktion.

[http://www.physics.ucdavis.edu/Classes/Physics9B_Animations/ReflRefr.html]

Diffraktion

Die Beugung oder Diffraktion ist die Ablenkung von Wellen an einem Hindernis. Durch Beugung kann sich eine Welle in den Raumbereichen ausbreiten, die auf rein geradem Weg durch das Hindernis versperrt wären. Zur Beugung kommt es durch Entstehung neuer Wellen entlang einer Wellenfront gemäß dem huygens-fresnelschen Prinzip. Diese können durch Überlagerung zu Interferenzerscheinungen führen.

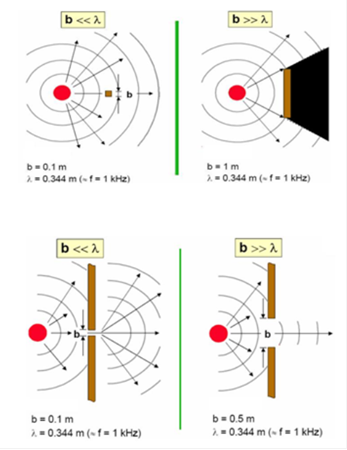
Abbildung. Abbildungen zeigen die Abhängigkeit der Diffraktion/Diffusion im Zusammenhang von Wellenlänge und Größe.

[http://www.bksv.com/]

Abbildung. Diffusion durch ein Loch.

[http://www.phy.ntnu.edu.tw]

2.4 Nachhall

In einem geschlossenen Raum entstehen neben der direkten Welle auch indirekte Schallwege. Der Schall erreicht den Empfänger (Ohr, Mikrofone) durch den direkten Weg am schnellsten. Später und gedämpfter, indirekte Schallwege entstehen durch primäre und sekundäre Reflexionen. Die späteren, durch mehrere Reflexionen interferierenden Wellen verursachen die Nachhall, die "Halligkeit". Diese sind für die subjektive "Raumwahrnehmung" sehr wichtig.

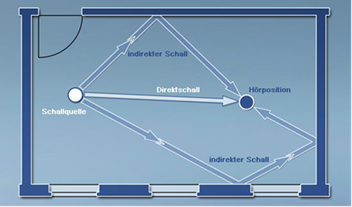
Abbildung. Direktschall und indirekter Schall in einem Raum.

[http://www.bksv.com/]

Die Nachhallzeit (T60 oder auch einfach RT) ist die bekannteste raumakustische Kenngröße. Unter der Nachhallzeit versteht man das Zeitintervall, innerhalb dessen der Schalldruck in einem Raum bei plötzlichem Verstummen der Schallquelle auf den tausendsten Teil seines Schalldruck-Anfangswerts abfällt, was einer Pegelabnahme von 60 dB entspricht.

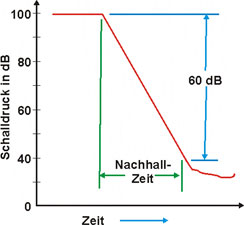
Abbildung. Die Nachhallzeit.

[http://www.renox.at]

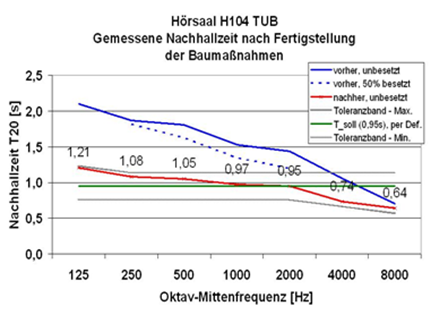
Abbildung. Beispiel für eine Nachhallzeitmessung in einem Hörsaal der TU Berlin.

[http://www.ak.tu-berlin.de/menue/forschung/forschungsprojekte/wellenfeldsynthese/raumakustische_konzeption]

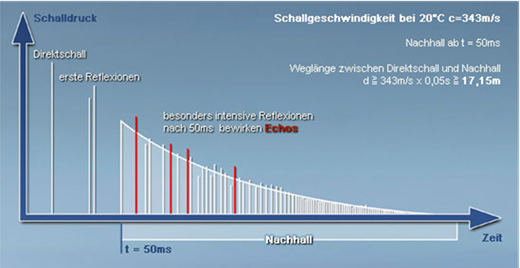
Abbildung. Darstellung von Nachhall. Wenn Entfernungen grösser als 17 m in einem Raum entstehen bekommen wir Echo.

[http://www.bilder-plus.de/nachhall.php]

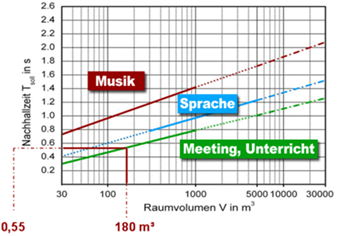
Abbildung. Nachhallzeit als Funktion von Baugröße.

[http://www.akustikkunst.de/raumakustik/raumakustische-grundlagen.html]

2.5 Berechnung der Nachhallzeit

Die Nachhallzeit kann gemessen und/oder mathematisch eingeschätzt werden. Es gibt zwei wichtige Formeln.

RT ist abhängig von: Raumvolumen (V) und Absorption (A). Wenn RT nicht zu klein ist kann man die Sabine-Formel anwenden:

wo RT ergibt sich in [sec], wenn V ist m³ und A ist m². Die Dimension von 0,161 ist [s/m].

A ist hier nicht die Oberfläche, sondern:

wo S ist Oberfläche in m².

Der Absorptionskoeffizient Alfa ist in der Praxis vorgegeben (Tabellen). Es kann sowohl gemessen oder kalkuliert werden:

Alfa = absorbierte Energie/einfallende Energie.

Alfa ist frequenzabhängig. Diese Formel ist für größeren RTs verwendbar (isotrope Bestrahlung vorausgesetzt, Raummoden vernachlässigt). Je grösser A oder kleiner RT ist, umso ungenauer das Ergebnis wird.

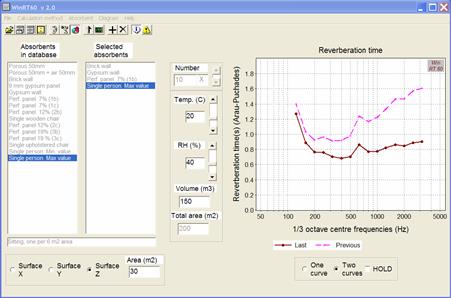
Abbildung. Es gibt viele Anwendungen für Nachhallzeitberechnungen (Screenshot WinRT60).

[http://www.nvo.com/winmls/winrt60/]

Für kleinere RTs ist die Eyring-Formel anwendbar:

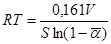
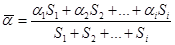
mit einem gemittelten Alfa:

und

Das Ergebnis ist genau, wenn die Alfas sind gleich groß (Nachteil). Es ist aber mathematisch korrekt, da für den schalltoten Raum (Alfa = 1) RT null ist.

*******************************************************************************************************************************************

3. Das Gehör und die Wahrnehmung von Vibrationen

3.1 Das Hörorgan

Die Wahrnehmung von akustischen Signalen wird davon mitbestimmt, wie Schallschwingungen auf ihrem Weg vom Außenohr über das Mittelohr hin zu den Nervenzellen des Innenohrs jeweils umgeformt und verarbeitet werden.

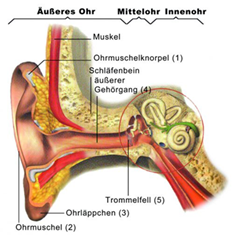
Abbildung. Aufbau des menschlichen Ohres

[http://www.organmodelle.de/ohrmodell.html]

Abbildung. Aufbau des Innenohres.

[http://www.organmodelle.de/ohrmodell.html]

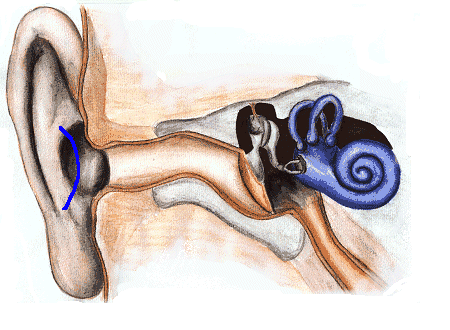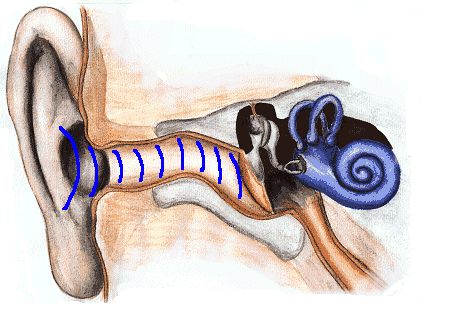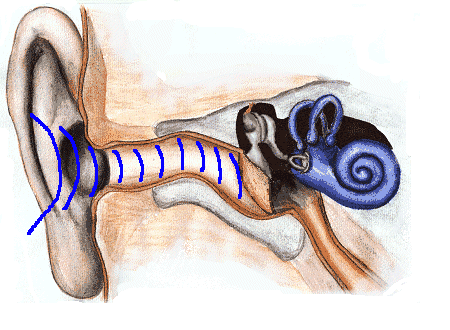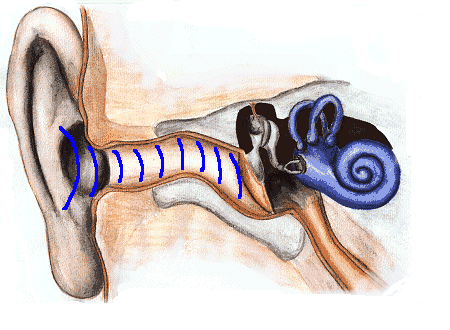
amittelohr1

Abbildung. Animation über die Funktionsweise des Aussenohres.

[http://www.dasp.uni-wuppertal.de/ars_auditus/physiologie/mittelohr1.htm]

Weitere Videos finden Sie hier: http://www.youtube.com/watch?v=FZHeXwb65JA, http://www.youtube.com/watch?v=tVEe_dXamtQ

3.2 Die Hörfläche

Die Hörfläche, auch Hörbereich oder Hörfeld, ist jener Frequenzbereich und Pegelbereich von Schall, der vom menschlichen Gehör wahrgenommen werden kann. Die Hörfläche kann auch das individuelle Hörvermögen eines einzelnen Menschen beschreiben. Die Hörfläche wird unten (d. h. für niedrige Pegel) von der Hörschwelle, also dem gerade noch hörbaren Schalldruckpegel, und oben von der Schmerzschwelle bestimmt. Links wird die Hörfläche von der tiefsten vom Menschen hörbaren Frequenz mit etwa 16 Hz bis 21 Hz und rechts von der höchsten hörbaren Frequenz mit etwa 16kHz bis 20 kHz begrenzt. Die Unbehaglichkeitsschwelle liegt auf der Hörfläche etwas unterhalb der Schmerzschwelle und ist ebenfalls frequenzabhängig. Die Hörschwelle liegt zwischen 2000 Hz und 5000 Hz am niedrigsten, dort hört der Mensch also am besten, hier treten auch die meisten Laute der gesprochenen Sprache auf.

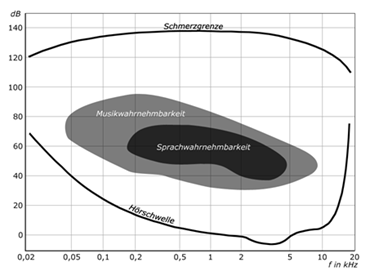
Abbildung. Die Hörfläche.

[hoerflache.png, wikipedia.org]

3.3 Die Lautheit

Die Lautheit ist eine durch Normen festgelegte Größe zur proportionalen Abbildung des menschlichen Lautstärkeempfindens. Die Maßeinheit der Lautheit ist sone. Die Lautheit verdoppelt sich, wenn der Schall als doppelt so laut empfunden wird. Es ist ein psychoakustischer Begriff. Es ist empfehlenswert zu merken, dass eine Erhöhung von ca. 6-10 dB des Schalldruckpegels resultiert in der Verdopplung von der subjektiven Lautheit ("zweimal so laut")! Lautstärkepegel in phone ist eine andere Größe. Für die Umrechnung gilt:

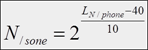
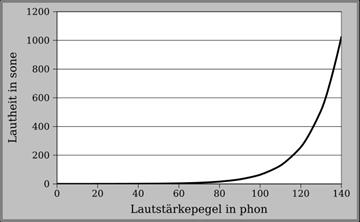
Abbildung. Umrechnung zwischen Phone und Sone.

[http://de.wikibooks.org/wiki/Grundlagen_der_Akustik:_Lautst%C3%A4rke_und_Lautheit]

Equal-Loudness Levels, also die Kurven der gleichen Lautstärke zeigen Phone-Kurven wo Schallereignisse die gleiche Empfindung von Lautstärke geben.

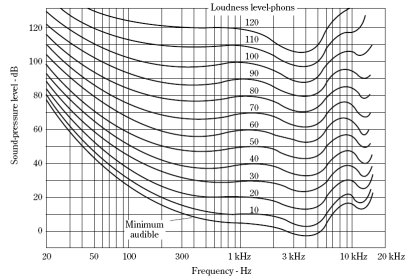
Abbildung. Kurven der gleichen Lautstärke.

[http://www.edn.com/design/audio-design/4015888/Using-the-Decibel--Part-5-The-Phon-Audible-Frequency-Range-and-THD]

3.4 Das Richtungshören

Richtungshören (räumliches Hören, akustische Lokalisation) ist die Fähigkeit, die Richtung einer Schallquelle zu bestimmen. Richtungshören erfolgt im allgemeinen durch den Vergleich des auf zwei am Körper unterschiedlich platzierten Ohren auftreffenden Schalls wird daher auch binaurales Richtungshören genannt). Zur neuronalen "Berechnung" der Schallrichtung werden folgende Kriterien herangezogen:

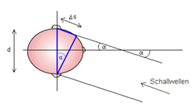
Die zeitliche Differenz, d.h. die Zeitspanne, die zwischen dem Ankommen einer Schallwelle am linken bzw. rechten Ohr liegt, wenn sich die Schallquelle seitlich des Hörers befindet (Interaural Time Difference, ITD).

Abbildung. Erstehung von ITD.

[http://www.dasp.uni-wuppertal.de/ars_auditus/ueberfunktion/funk24.htm]

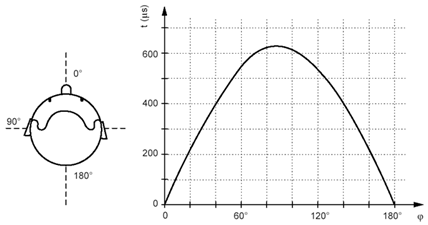
Abbildung. ITD als Funktion von Winkel.

[Wersényi Gy. – Pszichoakusztika és az emberi térhallás alapjai, 2012, Universitas Kiadó]

Die Differenz des Schalldrucks. Die von einer seitlich vom Hörer befindlichen Schallquelle ausgesandten Schallwellen werden auf dem Wege zu dem der Schallquelle abgewandten Hörorgan beim Durchtritt durch den Schädel gedämpft (Interaural Level Difference, ILD).
Unterschiede in der Klangfarbe. Diese resultieren daraus, dass beim Durchtritt durch den Schädel höhere Töne stärker gedämpft werden als tiefere. Außerdem beeinflusst die Form der Ohrmuschel je nach Richtung des Schalls dessen Klangfarbe, wodurch auch monaurales Richtungshören möglich wird. Dieses wird durch die Aussenohrübertragunsfunktionen (HRTF) beschrieben.

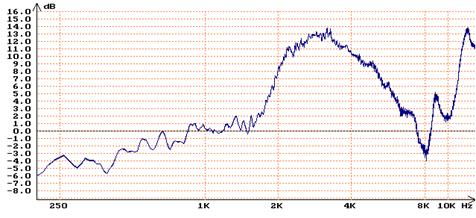
Abbildung. HRTF von einem Ohr aus der Richtung "vorne". Schallwellen werden mit diesem "Filter" richtungsabhängig gefiltert.

[Wersényi Gy. – Pszichoakusztika és az emberi térhallás alapjai, 2012, Universitas Kiadó]

Abbildung. Kunstköpfe für binaurale Messungen und Aufnahmen.

[http://www.isvr.co.uk/audioetc/earsimulators.htm]

3.5 Verdeckung

Maskierungseffekte (auch Verdeckung genannt) bewirken beim menschlichen Gehör, dass der Mensch in einem Geräusch bestimmte Frequenzanteile nicht oder nur mit verringerter Sensitivität wahrnehmen kann. Interferenz von Signalen können also Verdeckung verursachen. Laute tiefere Frequenzen überdecken leise höhere Frequenzen. Es wird auch in digitale Kodierungen genutzt, z.B. MP3-Kodierung kann bis zu 12:1 Datenreduktion führen.

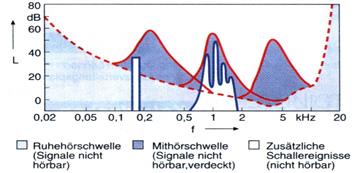
Ausschnitt1

Abbildung. Verdeckung von Sinustönen.

[http://www.fh-wedel.de/]

3.6 Subjektive Vibroakustik

Subjektives Schwingungsempfinden ist in der Akustik ebenso wichtig. Im Fall von mechanischen Schwingungen kann es eine Störung bei hohen Amplituden und längerer zeitlicher Einwirkung zu gesundheitlichen Beeinträchtigungen kommen. Die Empfindlichkeit eines Menschen auf Schwingungseinwirkung kann psychophysisch bestimmt werden. Wenn wir die Beschleunigung in dB angeben möchten, ist der Bezugswert REF=10^-6 m/s² und L = 20 log (a/REF). Die Empfindlichkeit des Menschen ist bezüglich Schwingungen im Bereich zwischen 4 und 10 Hz am größten. Die noch wahrnehmbare Vibrationspegel-Unterschiedsschwelle ist ca. 1,6 dB.

Die Empfindung ist abhängig von der Schwingungsfrequenz. Tieffrequente Schwingungen bis ca. 50 Hz werden vom Menschen bei körperlichem Kontakt unmittelbar als Vibration wahrgenommen. Schwingungen bis ca. 1 kHz sind als Körperschall immer noch von Bedeutung (wenn durch ihn Luftschall angeregt wird der auch vom Ohr wahrgenommen wird). Zwischen 20 und 100 Hz sind Schwingungen sowohl hörbar als auch fühlbar. Das nennt sich "Rauheit" (Harshness).

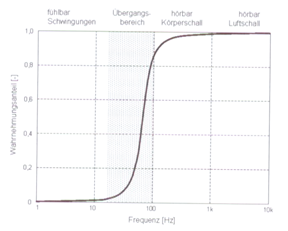
Abbildung. Vibroakustische Wahrnehmungsbereiche.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

*******************************************************************************************************************************************

4. Mechanische und akustische Elemente

4.1 Elemente und Netzwerke

Akustische Netzwerke können wie die elektrischen und mechanischen Netzwerke dargestellt und modelliert werden. Akustik ist ein Teil der Mechanik.

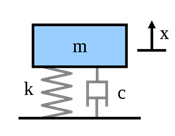
File:Mass spring damper.svg

Abbildung. Masse-, Feder-, Dämpfer-System.

[http://de.wikipedia.org/wiki/Erzwungene_Schwingung]

Ein gutes Beispiel sind Mikrofone und Lautsprecher besitzen einen elektromechanischen Wandler, welcher die mechanischen Schwingungen in elektrische Schwingungen umwandeln, oder umgekehrt.

4.2 Modelle mit konzentrierten Systemparametern

In der Elektronik gibt es:

reine Induktivität (L, Spule);
reine Kapazität (C, Kondensator); und
realer, frequenzunabhängiger Verlust in Form von Widerständen (R),
und die Impedanzen.

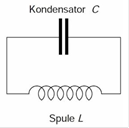
In der Mechanik gibt es:

Masse (m),
Feder (C) und
mechanischer Widerstand (R).

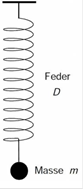
Statt Federkonstante D beschreiben wir einen Feder mit der reziproke Federkonstante ("Steifigkeit"): C=1/D. Ein solches System nennt man auch Feder-Masse-Systeme.

4.3 Resonanz

Resonanz ist in Physik und Technik das verstärkte Mitschwingen eines schwingungsfähigen Systems. Bei periodischer Anregung muss die Anregungsfrequenz in der Nähe einer Resonanzfrequenz des Systems liegen. Ist das System nicht zu stark gedämpft, kann es dabei um ein Vielfaches stärker ausschlagen (Resonanzüberhöhung) als in dem Fall, dass dieselbe Anregung nicht periodisch, sondern mit konstanter Stärke einwirken würde. Das Phänomen kann bei allen schwingfähigen physikalischen und technischen Systemen auftreten.

In der Elektronik benutzt man Induktivität und Kapazität für einen verlustfreien Resonator: die Energie oszilliert in sinusförmigen Wellen. In der Mechanik sind es Masse und Feder. Ein Federpendel oder Federschwinger ist ein harmonischer Oszillator, der aus einer Schraubenfeder und einem daran befestigten Massestück besteht, welches sich geradlinig längs der Richtung bewegen kann, in der Feder sich verlängert oder verkürzt. Sofern sich die Masse in Lotrichtung bewegt, beeinflusst die Schwerkraft die Ruhelage. Beim Loslassen des aus seiner Ruhelage ausgelenkten Federschwingers beginnt eine harmonische Schwingung, die bei fehlender Dämpfung nicht mehr abklingt.

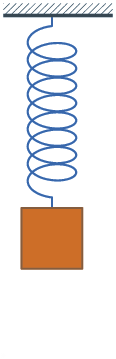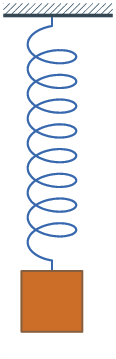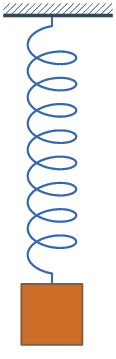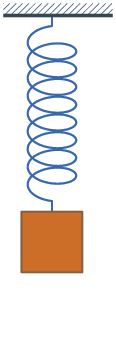
Abbildung. Feder-Masse-System

[http://en.wikipedia.org/wiki/Vibration]

Die ideale Masse ist:

inkompressibel, d.h. jeder Punkt der Masse bewegt sich mit der gleichen Geschwindigkeit.
Beschreibungsgleichung: F = ma (Newton Gesetz).

Die ideale Feder ist:

Steifigkeit unabhängig von der Auslenkung.
Beschreibungsgleichung: F = sx (Hookesches Gesetz).
über der Feder fällt keine Kraft ab.

Der Ideale Reibwiderstand:

Geschwindigkeitsproportionale Reibung.
Beschreibungsgleichung: F = Ru.
Über dem Reibwiderstand fällt keine Kraft ab.

Die mechanische Quellen sind entweder Kraftquellen (Kraft ist unabhängig von Geschwindigkeit) oder Geschwindigkeitsquellen (Geschwindigkeit ist unabhängig von Kraft).

In der Akustik ist es auch Masse und Federung.

Die akustische Masse ist:

Beschleunigte aber nicht komprimierte Luft.
Realisierung: Röhrchen mit Länge (l), Durchmesser (d), wobei d<<l<<λ.
Alle Teilchen der Luft bewegen sich gleichzeitig.

Abbildung. Abbildung zeigt stehende Wellen in einem geöffneten Röhrchen: longitudinale akustische stehende Wellen in einem Röhrchen mit Öffnungen an beiden Enden (akustische Masse). Oben sieht man die größte Wellenlänge (Grundfrequenz) welche sich bilden kann. Die Auslenkung hat Knoten (Nullpunkt) in der Mitte und Maxima am Ende des Röhrchens. Die Entfernung entspricht hier halber Wellenlänge. Die beiden anderen Bilder zeigen höhere harmonische (zweite und dritte).

[http://www.acs.psu.edu/drussell/demos.html]

Die akustische Federung ist:

komprimierte aber nicht beschleunigte Luft.
Realisierung: Hohlraum (Volumen V) mit größter Abmessung (l), wobei l<< λ.
adiabatisches Verhalten (kein Temperaturausgleich).
Position der Öffnung des Volumens ist unbedeutend.

Abbildung Stehende Wellen in einem Hohlraum: longitudinale akustische stehende Wellen in einem Hohlraum mit Öffnung nur an einem Ende (akustische Federung). Oben sieht man die größte Wellenlänge (Grundfrequenz) welche sich bilden kann. Die Auslenkung hat Knoten (Nullpunkt) an der Wand und Maximum an der Öffnung. Die Entfernung entspricht einer Viertel der Wellenlänge. Die beiden anderen Bilder zeigen die nächsten zwei harmonischen (dritte und fünfte).

[http://www.acs.psu.edu/drussell/demos.html]

Der akustische Widerstand ist:

Verlustelement, wandelt Schallenergie in Wärme um.
Realisierung: poröse Materialien, Siebe.
akustischer Widerstand eines engen Röhrchens ist immer auch von einer akustischen Masse begleitet.
für kleine Durchmesser und tiefe Frequenzen kann die Wirkung der Masse vernachlässigt werden.

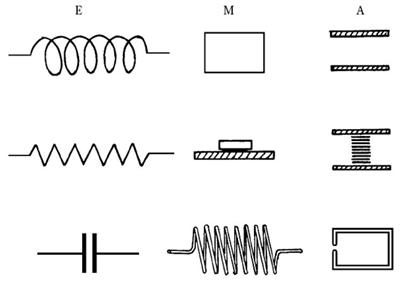
Abbildung. Potenzial- und Flussgrössen.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

Die Eigenfrequenz eines schwingfähigen Systems ist eine der Frequenzen mit der das System nach einmaliger Anregung schwingen kann (bei Vernachlässigung der Dämpfung). Wenn einem solchen System von außen Schwingungen aufgezwungen werden deren Frequenz mit einer der Eigenfrequenzen übereinstimmt reagiert das System mit besonders großen Amplituden was man als Resonanz bezeichnet. Eigenfrequenzen aus der Elektronik, Mechanik und Akustik:

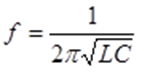
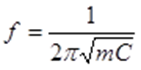
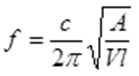
Ein Helmholtz-Resonator ist ein akustischer Resonator. In der Akustik ist die akustische Masse und Federung für einen Resonator nötig. Ein Helmholtz-Resonator hat eine Masse und eine Federung, d.h. einen Hohlraum und ein Röhrchen zusammengeknüpft. Ein solcher Resonator funktioniert als Absorber an der Resonanzfrequenz, wo c ist Schallgeschwindigkeit, A ist Oberfläche des (Flaschen)halses, l ist die Länge des Halses, V ist Volumen. Wir müssen annehmen, dass V >> Al.

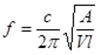
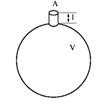
Abbildung. Helmholtz-Resonator (Flasche mit Hals).

[http://fisicaondemusica.unimore.it/Risuonatori_di_Helmholtz_en.html]

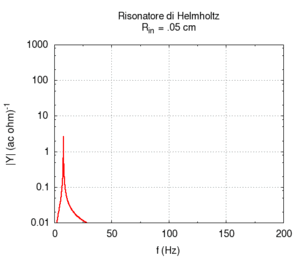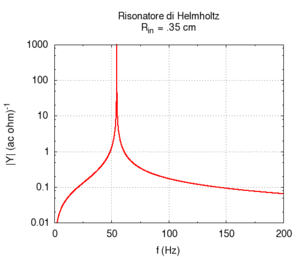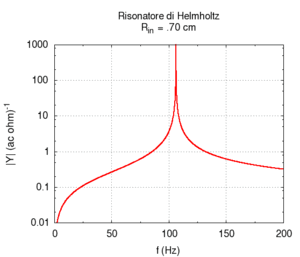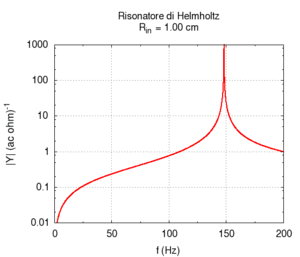
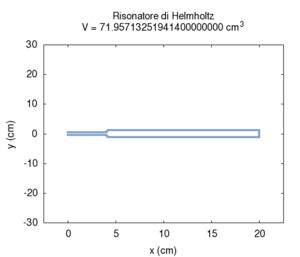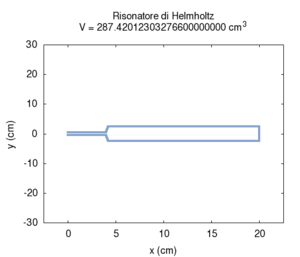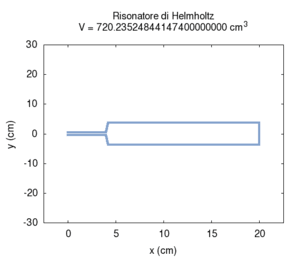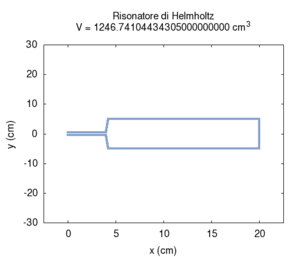
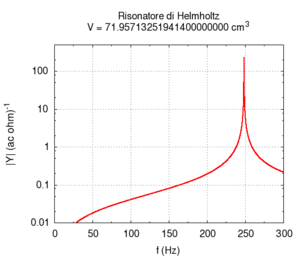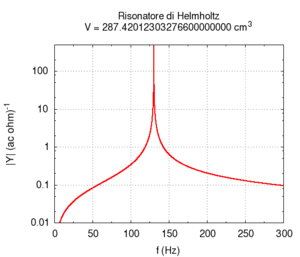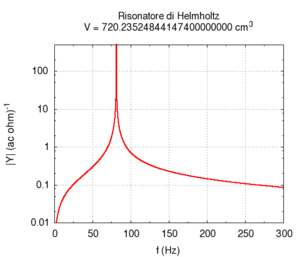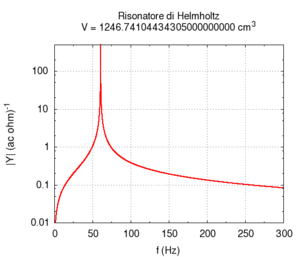
Abbildung. Veränderung der Eigenfrequenz eines Helmholtz-Resonators als Funktion vom Hals (oben) bzw. Volumen (unten). [http://www.phys.unsw.edu.au/jw/Helmholtz.html] [http://fisicaondemusica.unimore.it/Risuonatori_di_Helmholtz_en.html

]

4.4 Interferenz

Interferenz beschreibt die Überlagerung von zwei oder mehr Wellen nach dem Superpositionsprinzip (Addition ihrer Amplituden). Es zur vollständigen destruktiven oder konstruktiven Interferenz führen.

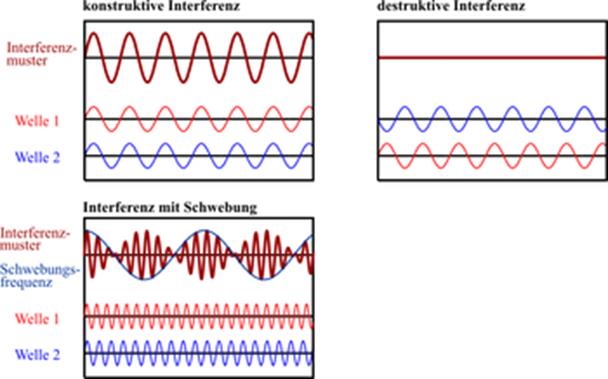
Abbildung. Interferenz zweier Wellen.

[http://neu.8goals4future.at/DE_WIKIPEDIA_O/WIKI/INTERFERENZ_PHYSIK_.HTM]

Eine stehende Welle entsteht aus der Überlagerung zweier gegenläufig fortschreitender Wellen gleicher Frequenz und gleicher Amplitude. Die Wellen können aus zwei verschiedenen Erregern stammen oder durch Reflexion einer Welle an einem Hindernis entstehen. Bei einer stehenden akustischen Welle ist das Medium nicht im Ruhestand, aber Maxima und Minima der Schalldrucks und Teilchengeschwindigkeit verschieben sich nicht. Die Knotenpunkte haben eine Entfernung von einer halben Wellenlänge. Solche stehende Wellen entstehen an Mediengrenzen, wo reflektierte Wellen mit den direkten Wellen aufeinander treffen. In der Praxis ist eine Wand weder "fest" noch "weich". In diesem Fall wird ein Teil der Wellenenergie absorbiert und nur mit geschränkter Amplitude reflektiert.

Abbildung. Entstehung einer stehenden Welle.

[http://www.physics.ucdavis.edu/Classes/Physics9B_Animations/SinesCollide.html]

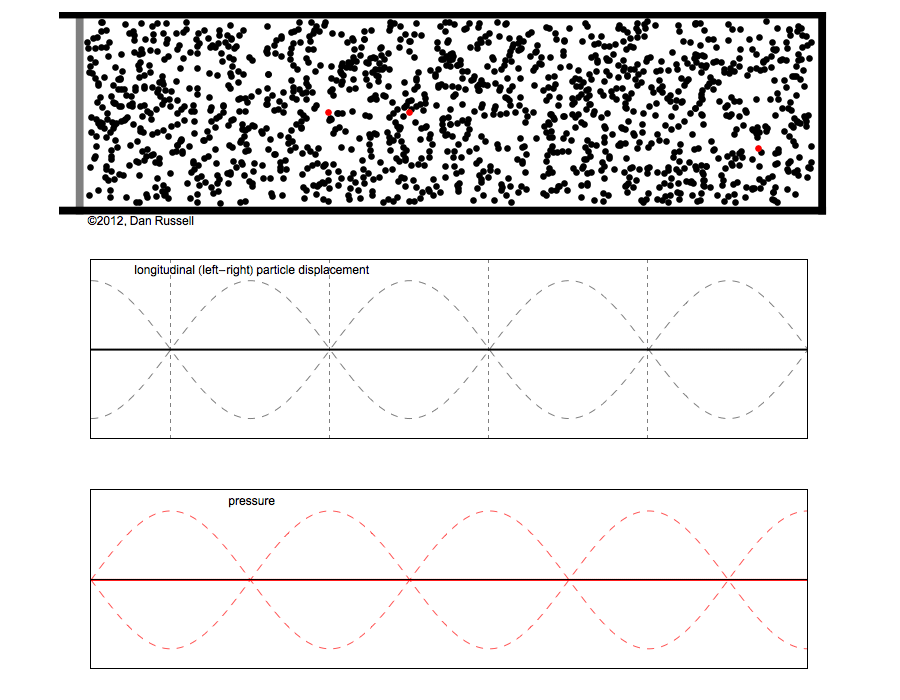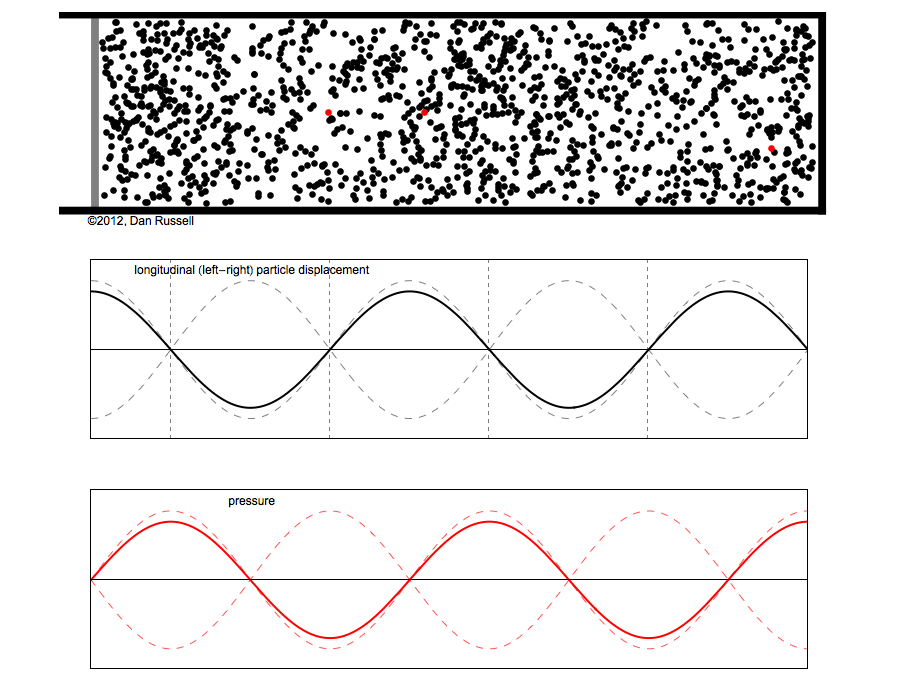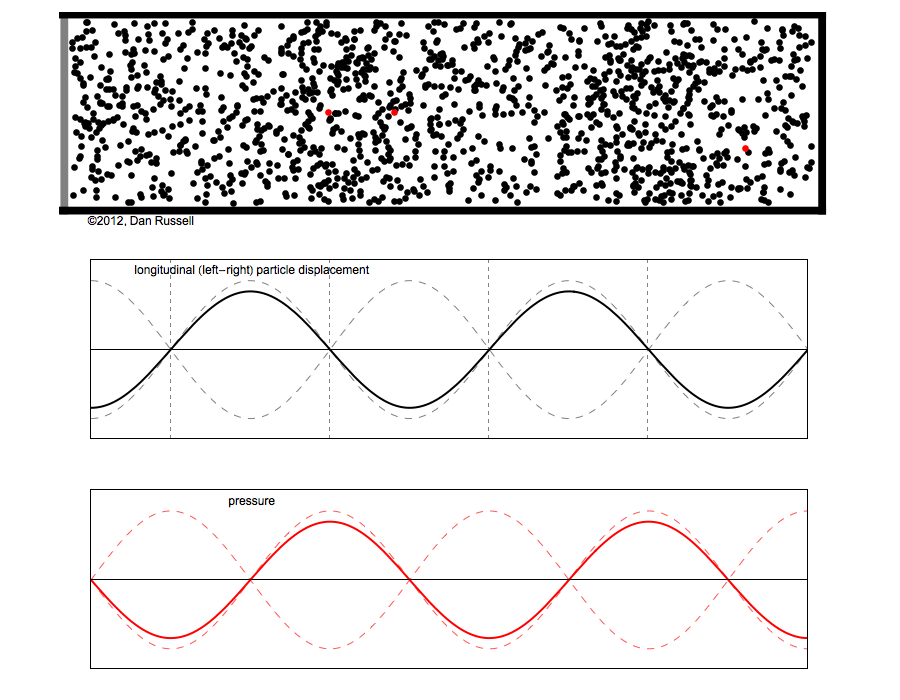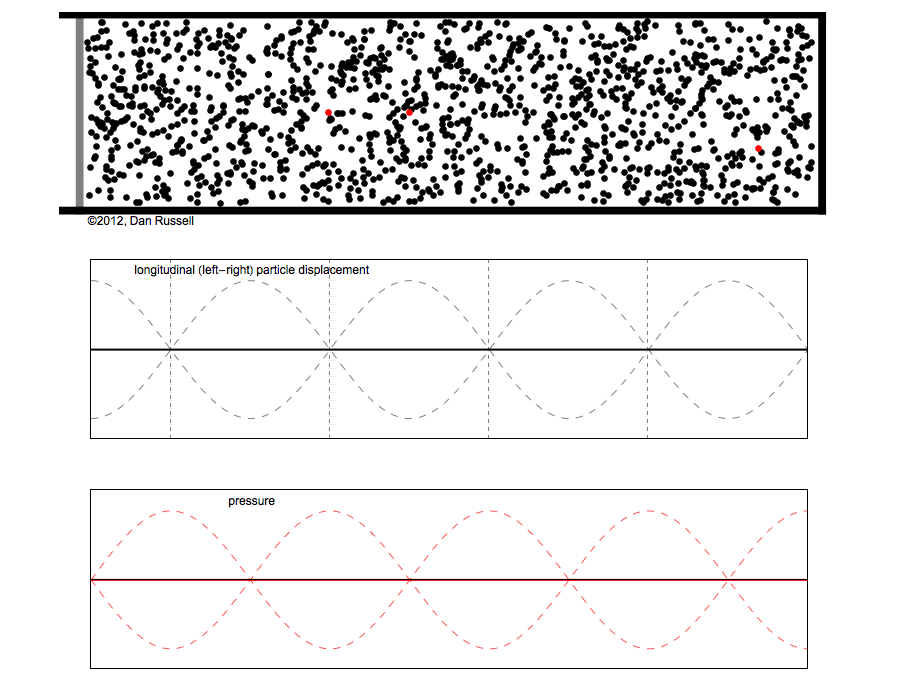
Abbildung. Schalldruck und Auslenkung bei einer stehenden Welle.

[http://www.acs.psu.edu/drussell/demos.html]

Abbildung. Harte und weiche Grenze.

[http://www.acs.psu.edu/drussell/demos.html]

4.5 Moden

Zwischen zwei Reflektoren können sich nur stehende Wellen mit bestimmten Wellenlängen bilden. Alle möglichen Wellenlängen werden als Eigenfrequenzen oder Eigenresonanzen bezeichnet. Welche Randbedingung dazu führt, dass die Wellenlängen nicht beliebig sein können, hängt von der Art der betrachteten Welle ab. z.B. muss bei fest eingespannten Enden einer schwingenden Saite an beiden Enden jeweils ein Schwingungsknoten vorliegen. Bei einer stehenden (akustischen) Longitudinalwelle tritt an jeder reflektierenden Wand in einem Raum immer ein Schalldruckbauch auf (Raummoden).

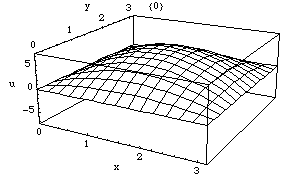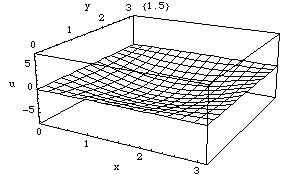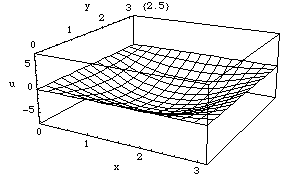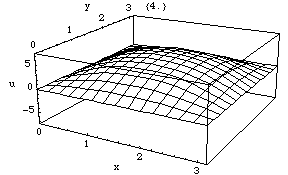
Abbildung. Raummode.

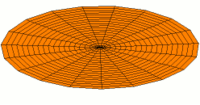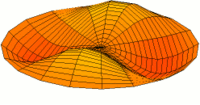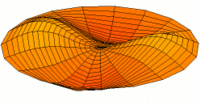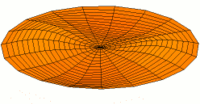
Abbildung. Moden bei einer schwingenden Platte.

[http://de.wikipedia.org/wiki/Moden]

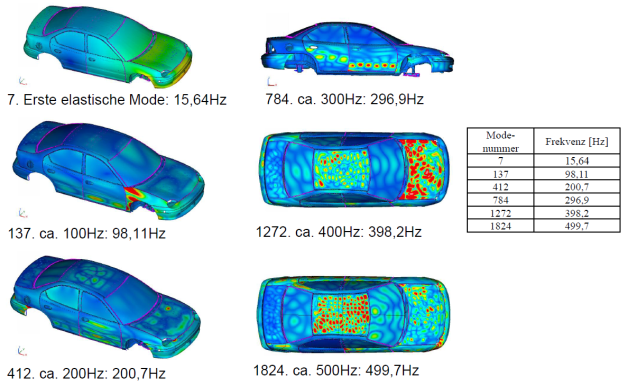
Abbildung. Moden eines Fahrzeugs.

[AUDI]

*****************************************************************************************************************************************

5. Akustische Elemente

5.1 Mikrofone

Ein Mikrofon ist ein Schallwandler, der Luftschall als Schallwechseldruckschwingungen in entsprechende elektrische Spannungsänderungen als Mikrofonsignal umwandelt. Erwartung ist ein breiter Frequenzumfang, hohe Empfindlichkeit und eine Umwandlung frei von Verzerrungen. Das Herz jedes Mikrofons ist der elektromechanische Wandler: elektrodynamisch oder Kapazität (kondensator) Typ.

Die Empfindlichkeit (Sensitivität) eines Mikrofons ist die Ausgangsspannung im Verhältnis zum einfallenden Schalldruck. Gemessen wird es bei 1 kHz in der Symmetrieaxe in [mV/Pa] oder dB.

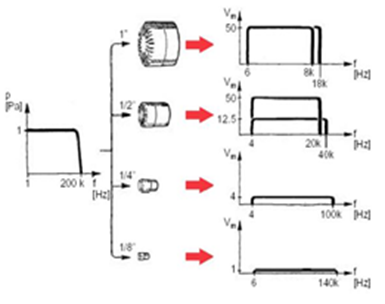
Abbildung. Zusammenhang zwischen Frequenzbereich und Empfindlichkeit.

[http://www.bksv.com/]

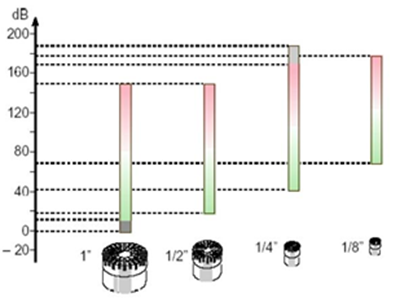
Abbildung. Zusammenhang zwischen Empfindlichkeit und Membrandurchmesser.

[http://www.bksv.com/]

Die Übertragungsfunktion ist die Empfindlichkeit als Funktion der Frequenz. Messmikrofone sind "flach" (frequenzunabhängig). Die Richtcharakteristik beschreibt in Form eines Polardiagrams die Empfindlichkeit des Mikrofons. Es ist die Ausgangsspannung im Verhältnis zum Schalldruck, in Abhängigkeit vom Schalleinfallswinkel.

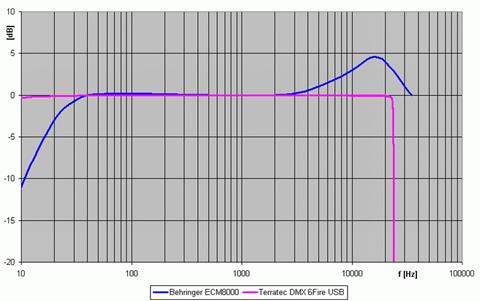
Abbildung. Übertragungsfunktionen von Mikrofonen.

[http://www.stroemlinge.de/index_AstraHGTC_Musikanlage_SPLMessung.html]

Abbildung. Messung für Mikrofone im schalltoten Raum.

[http://www.schalllabor-hamburg.de/technische-akustik]

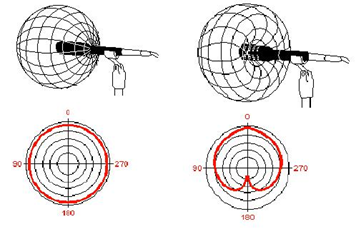
Abbildung. Richtcharakteristik: Kugel und Niere.

[http://audioclassroom.wordpress.com/2014/05/21/how-to-use-microphone-pickup-patterns/]

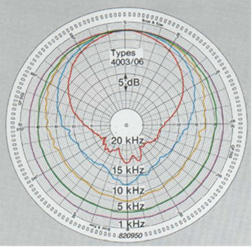
Abbildung. Veränderung der Richtcharakteristik mit der Frequenz.

[http://www.bksv.com/]

Mikrofone wandeln Schallereignisse erst in mechanische Energie und anschließend in elektrische Energie um. Schall breitet sich im Medium Luft durch Schwingen der Luftmoleküle aus. Die dabei entstehenden Druckänderungen versetzen eine ins Schallfeld eingebrachte, gespannte Membran in mechanische Schwingungen. Bei dem bekanntesten dynamischen Mikrofontyp ist diese Membran mit einem Spulenkörper verbunden. Die Spule bewegt sich in einem statischen Magnetfeld und erzeugt nach dem Induktionsgesetz an ihren Anschlüssen eine vom Schalldruck abhängige Wechselspannung. Das Induktionsgesetz in der allgemeiner Form ΔU = -B · l · Δv zeigt, dass die induzierte Wechselspannung ΔU direkt proportional zur Änderungsgeschwindigkeit Δv ist. Sie steht im direkten Zusammenhang mit den Druckänderungen, die von der Schallquelle ausgehen. Bei gleicher mechanischer Erregung wird eine höhere Nutzspannung induziert, je größer die magnetische Flussdichte B des Magnetfelds ist und je mehr Windungen der Spule (n · l) im Magnetfeld bewegt werden. Für eine Animation und weitere Information siehe: http://elektroniktutor.oszkim.de/akustik/mikrofon.html.

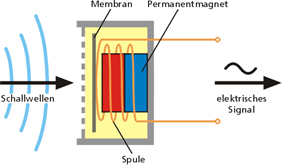
Abbildung. Dynamisches Mikrofon (Prinzip und Abbildung).

[http://www.holmco.de/mikg.html]

Das Kondensatormikrofon nutzt die durch Abstandsänderungen zwischen der (beweglichen) Membran und der Gegenelektrode hervorgerufene Kapazitätsänderungen, um je nach Ausführung Schalldruck oder Schallschnelle in ein elektrisches Signal umzuwandeln. Hier ist eine wenige Mikrometer dicke, elektrisch leitfähige Membran dicht vor einer - aus akustischen Gründen oft gelochten - Metallplatte elektrisch isoliert angebracht. Technisch betrachtet ist diese Anordnung ein Plattenkondensator mit Luft-Dielektrikum, der eine elektrische Kapazität von etwa 20 bis 100 pF besitzt. Die Kapazität C des Kondensators ist abhängig von der Plattenfläche A und dem Abstand d der Kondensatorplatten. Eintreffender Schall bringt die Membran zum Schwingen, wodurch sich der Abstand zwischen Membran und Gegenelektrode und damit auch die Kapazität des Kondensators verändert.

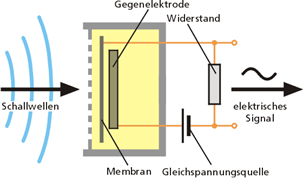
Abbildung. Kondensatormikrofon (Prinzip und Abbildung).

[http://www.bksv.com/]

Allgemein kann man dynamische Mikrofone wie folgend charakterisieren:

elektrodynamischer Wandler,
allgemeine Anwendungen, Aufnahmetechnik (Studio und Live),
relativ preisgünstig,
relativ schmale Bandbreite,
keine Spannungsversorgung nötig (passiv).

Allgemein kann man Kondensator Mikrofone wie folgend charakterisieren:

kapazitive Wandlerprinzip,
für Messungen und Studioaufnahmen geeignet,
teuer,
breitbandige Übertragung,
Spannungsversorgung üblicher Weise nötig (aktiv). Der Vorverstärker ist oft mit dem Mikrofon zusammengebaut.

5.2 Lautsprecher

Im Gegensatz zur Mikrofoneinsatz werden bei Lautsprecherwiedergabe fast nur dynamische Lautsprecher benutzt. ("Inverz Mikrofone"). Bei Lautsprechern werden elektrische Schwingungen in Schallschwingungen umgesetzt.

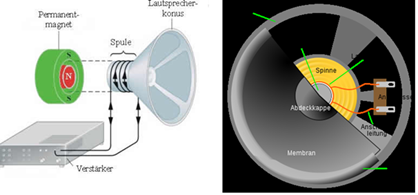
Abbildung. Dynamischer Lautsprecher.

[http://www.leifiphysik.de/web_ph10/umwelt-technik/09lautsprech/lautsprech.htm]

Die Empfindlichkeit eines Lautsprechers gibt den abgestrahlten Schalldruck im Verhältnis zur Eingangsspannung bei 1 kHz in Richtung "vorne" (in Pa/V oder in dB). Frequenzgang (Übertragungsfunktion) ist die Empfindlichkeit als Funktion der Frequenz. In der Praxis jedes Lautsprecher-Chassis (Tieftöner, Hochtöner, Mitteltöner) bekommt den Frequenzbereich zugeteilt (Frequenzweichen). Andere wichtige Parameter sind:

Richtcharakteristik
Nennbelastbarkeit: Die in Watt angegebene Nennbelastbarkeit des Lautsprechers gibt an, welche elektrische Leistung der Lautsprecher im Dauerbetrieb aufnehmen kann.
Die maximale thermische Belastbarkeit und der maximal zulässige Membranhub.
Die Musikbelastbarkeit umschreibt diejenige kurzfristige (max. 2 Sekunden) Impulsbelastbarkeit, die der Lautsprecher ohne Schäden am Material bewältigen kann.
Impedanz: In der Einheit Ohm angegebener Stromwiderstand. Verstärker mit niedriger Ausgangsimpedanz sind von Vorteil. Impedanz ist der gerundete Wert des Absolutwertes der gemessenen Impedanz auf 4, 6, oder 8 Ohm.

Lautsprecher müssen eingebaut werden wegen akustischem Kurzschluss. Ein akustischer Kurzschluss ist ein akustisches Phänomen verantwortlich dafür, dass Lautsprecher überhaupt Gehäuse benötigen.

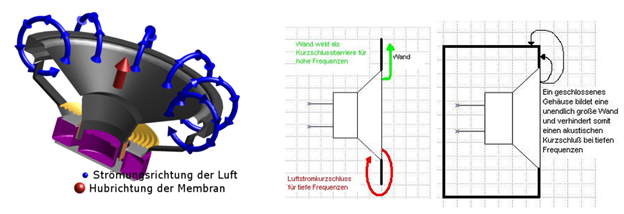
Abbildung. Akustischer Kurzschluss.

[www.hekko.de]

Schwingt die Membran nach vorn, wird vorderseitig die Luft verdichtet, während hinten "dünner" (Phasendifferenz von 180 Grad). Die Luft findet (bei tieffrequenten Schwingungen) ausreichend Zeit, druckausgleichend zwischen Vorder- und Rückseite hin und her zu strömen. Die gegenläufigen Wellen eliminieren sich. Um Lautsprechervorderseite und -rückseite muss akustisch isoliert werden. Mit Hilfe einer auf der Gehäuserück-, vorder- oder Unterseite befindlichen Austrittsöffnung wird der nach hinten austretende Schall des Basschassis genutzt.

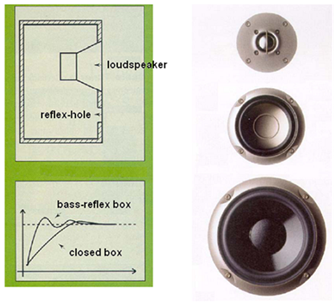
Abbildung. Mehrweg-Lautsprecher und Bassreflex-Ausstattung.

5.3 Beschleunigungssensoren

Der wichtigste Sensor im Bereich Schwingungsmessungen. Die Beschleunigung wird als auf eine Testmasse wirkende Trägheitskraft bestimmt (f = ma). Die ersten hatten eine so genannte "sensitive (empfindliche) Achse", auf der die Prüfmasse verschiebbar angeordnet war; später wurden sie durch genauere Systeme mit biegsamen Quarz-Stäben oder magnetisch stabilisierten Massen ersetzt. Miniaturisierte Sensoren sind meist mit piezoelektrischen Sensoren oder als MEMS (Micro-Electro-Mechanical System) aufgebaut. Viele technische Anwendungen benötigen 3D Messungen. Kleinsensoren mit einer Masse von wenigen Gramm haben Messbereiche von einigen g bis zu hunderten g. Die Auflösung erreicht 0,01mg. Präzisionsinstrumente mit einer Masse von mehreren Kilogramm liefern Genauigkeiten von 10^-9g.

Piezoelektrische Beschleunigungssensoren wandeln dynamische Druckschwankungen in elektrische Signale um. Die Druckschwankung wird durch eine an der Piezokeramik befestigte ("seismische") Masse erzeugt und wirkt bei einer Beschleunigung des Gesamtsystems auf die Piezokeramik (Feder-Masse System). Konstante Beschleunigungen (z. B. Erdbeschleunigung) können damit nicht erfasst werden.

Abbildung. Piezosensoren.

[http://www.sensorsmag.com/sensors/acceleration-vibration/simple-steps-selecting-right-accelerometer-1557]

[http://www.itwissen.info/definition/lexikon/MEMS-Sensor-MEMS-sensor.html]

[http://www.althen.de/beschleunigung/egcs-s425/]

Prinzip ist dass die Kraft bei konstanter Masse direkt proportional zur Beschleunigung wird: f = ma. Die seismische Masse im Sensor erzeugt somit bei Beschleunigung eine Kraftwirkung auf das piezoelektrische Material, welche in diesem wiederum eine proportionale Ladungsverschiebung zur Folge hat. Diese wird durch einen Verstärker in eine Spannung umgewandelt (auch proportional zur Beschleunigung). Ein Feder-Masse-System hat ein Tiefpassverhalten mit einem linearen Frequenzbereich und einer Resonanz. Je kleiner die Masse ist, umso größer ist die Resonanzfrequenz und kleiner die Empfindlichkeit.

Abbildung. Resonanz eines Sensors.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

Zu der Arbeit mit Sensoren gehört auch Fehler- und Datenbehandlung. Mögliche Fehlerquellen sind:

unebene oder raue Kontaktfläche,
Nachgiebigkeit der Kontaktfläche (bei Blech oder Kunststoff),
zu hohe Masse des Sensors,
lange Verbindungskabel.

TEDS steht für Transducer Electronic Data Sheet. Es ist eine standardisierte Methode für das Speichern von Wandlerdaten, Identifikation, Kalibration, Ausgleichinformation und Herstellerinformation. Jeder Wandler und Instrument kann sein eigenes TEDS-Datenblatt haben. Das TEDS kann als Speicher geknüpft zu dem Sensor implementiert werden.

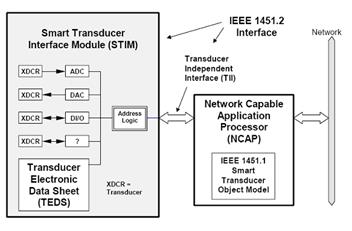
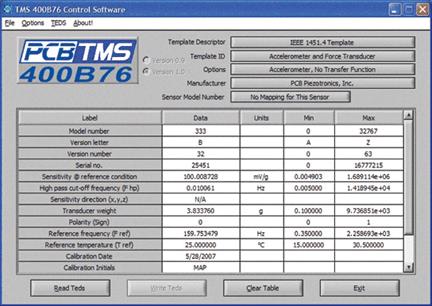
Abbildung. TEDS.

[http://archives.sensorsmag.com/articles/1097/ieee1097/]

[https://www.pcb.com/Aerospace/Ground_Test/TEDS.aspx]

MEMS steht für miniaturisierte Beschleunigungssensoren: Mikro-Elektro-Mechanische Systeme (MEMS) werden aus Silizium hergestellt. Diese Sensoren sind Feder-Masse-Systeme, bei denen die "Federn" nur wenige µm breite Silicium-Stege sind und auch die Masse aus Silizium hergestellt ist. Durch die Auslenkung bei Beschleunigung kann zwischen dem gefedert aufgehängten Teil und einer festen Bezugselektrode eine Änderung der elektrischen Kapazität gemessen werden. Der gesamte Messbereich entspricht einer Kapazitätsänderung von nur ca. 1 pF. So muss die Elektronik zur Auswertung auf demselben Halbleiterbaustein sein.

Abbildung. Ein MEMS Sensor.

[http://www.eeweb.com/news/mems-absolute-pressure-sensor]

Vorteile sind: relativ geringer Stückkosten (Massenfertigung) und hoher Zuverlässigkeit. Sensoren in MEMS-Technik werden nicht nur für die Messung der (linearen) Beschleunigung, sondern auch für die Messung der Winkelbeschleunigung hergestellt (so genannte Gyrosensoren).

Die Vibrationsprüfung ist ein Verfahren zur Untersuchung der durch schwingungsauftretenden Belastungen und ihre Folgen. In erster Linie wird dieses Verfahren verwendet, um die mechanische Festigkeit zu prüfen. Beispiel: elektronische Steuergeräte im Auto. Diese sind beim Fahren zwangsläufig Schwingungen verschiedener Frequenz und Amplitude ausgesetzt (z. B. Reifen, Straßenverhältnisse, Motorvibrationen durch Massenkräfte). Damit solch ein Fehler im Fahrzeug nicht im Betrieb eintritt, werden auf sogenannten Shakern die Vibrationsbeanspruchungen des späteren Einsatzfalles nachgebildet. In einem Shaker bewegt sich eine Spule im Magnetfeld und wandelt ein elektrisches Signal in eine mechanische Auslenkung um. Frequenzbereiche für die Vibrationsprüfung von Kfz- Elektronik sind: 10 - 1000 (2000) Hz. Typische Beschleunigungswerte sind für Karosseriebau 1 - 3 g, für Motorenbau 8 - 28 g. Für die Prüfung von sehr tieffrequenten Schwingungen werden hydraulische Shaker eingesetzt, die auch wesentlich größere Amplituden erzeugen können.

Abbildung. Verschiedene Shaker in der KFZ-Technik.

[http://www.qualtest.com/html/New_Vibration_Capability_LDS_V9_Electrodynamic_shaker.htm]

[http://www.lmsgermany.com/Inertia-Shaker-with-integrated-sensors]

Es können in der akustischen Messtechnik weitere Messmittel angewendet werden, wie z.B. impact hammer, omnidirectional sound source, reference sound source oder "start gun".

Abbildung. Weitere Messmittel in der Akustik.

[http://www.bksv.com/]

******************************************************************************************************************************************

6. Methoden der Analyse und Messtechnik

6.1 Grundlagen zur Messtechnik

Die Fourier-Analyse (FFT) ist die Zerlegung eines Zeitsignals in Sinusoiden zunehmender Frequenzen, sodass durch deren Summierung (=Fourier-Synthese) das Zeitsignal rekonstruiert wäre. Durch die Fourier-Analyse bekommt man ein Spektrum, das die Amplituden-Werte der Sinusoiden (in dB) als Funktion der Frequenz enthält.

Synthesis_square

[http://de.academic.ru/dic.nsf/dewiki/1164684]

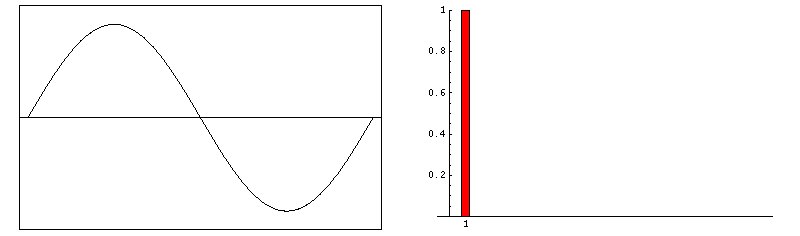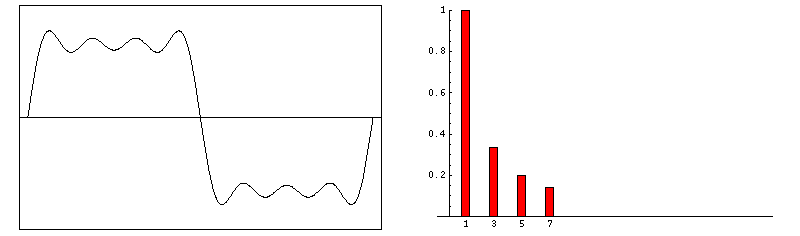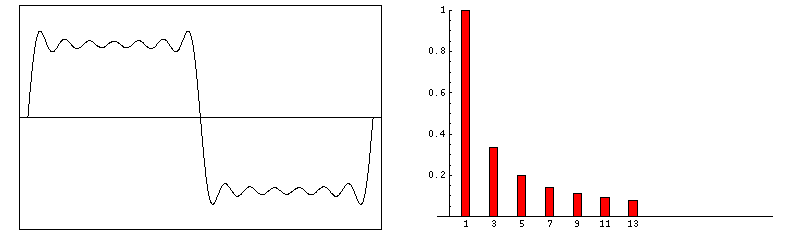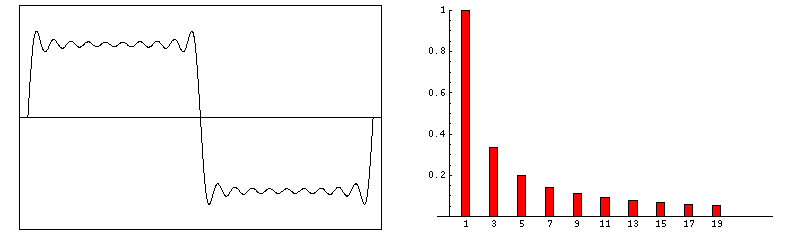
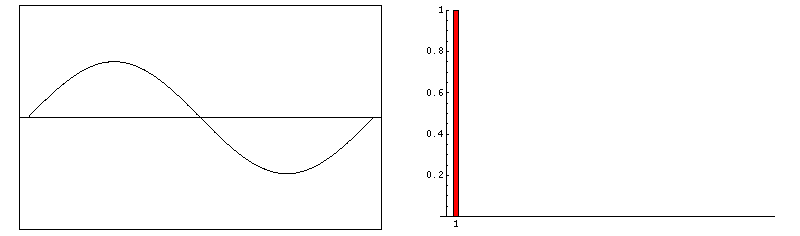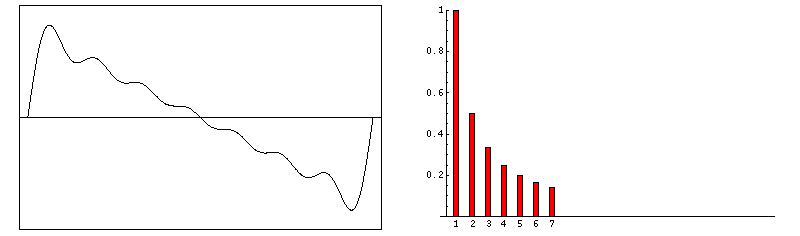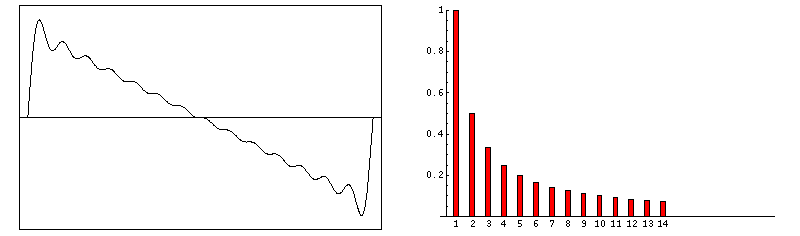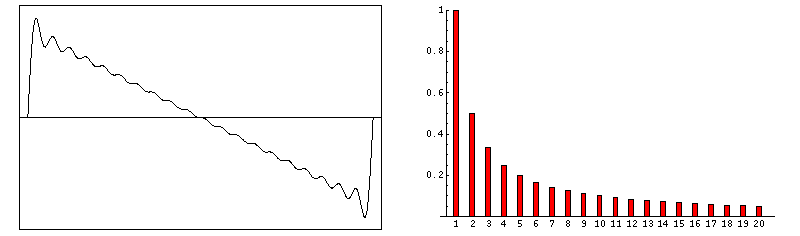
Abbildung. Entstehung von FFT Daten für verschieden Signale.

[www.acs.psu.edu]

Als Verzerrung bezeichnet man in der Elektrotechnik und in der Akustik eine nicht erwünschte Veränderung der Form im zeitlichen Verlauf einer zeitveränderlichen Größe. Sie wird überwiegend bei periodischen Signalen beobachtet; aber auch ein einzelner Impuls kann in seiner Form geändert, eben verzerrt werden. In der Akustik gibt es zur Erzielung gewisser Klangeffekte auch die gewollte Verzerrung. Man unterscheidet "lineare Verzerrungen" und "nichtlineare Verzerrungen".

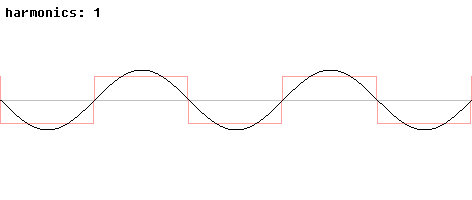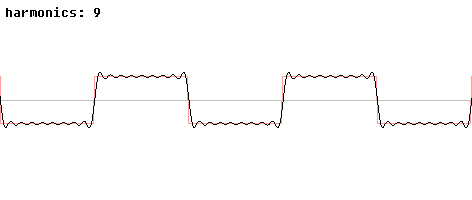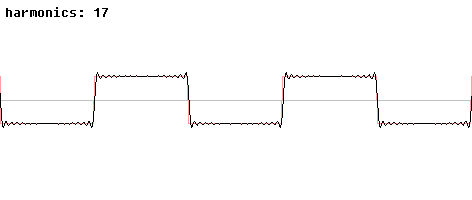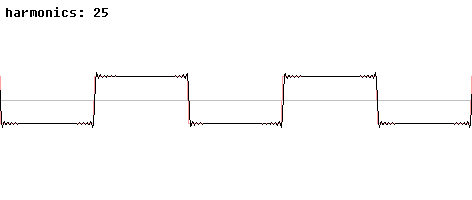
Die nichtlineare Verzerrung, verursacht durch ein nichtlineares System, wird vorzugsweise bei einer Abweichung von einem ursprünglich sinusförmigen Signalverlauf bedeutsam. Diese Art von Verzerrung lässt sich so beschreiben, dass sich zusätzliche Sinus-Schwingungen ausbilden, die als Oberschwingungen zur ursprünglichen Grundschwingung bezeichnet werden. Die Oberschwingungen weisen ganzzahlig-vielfach höhere Frequenzen als die Grundfrequenz auf. Die lineare Verzerrung entsteht in linearen Netzwerken durch deren Frequenzgang, wenn sich Verstärker und Übertragungswege zwar linear, aber frequenzabhängig verhalten.

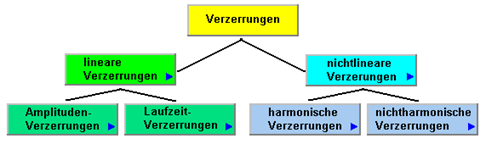
Abbildung. Verzerrungen.

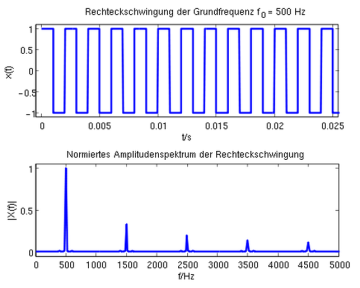
Abbildung. Nichtlineare Verzerrungen beim Rechtecksignal.

[http://de.wikipedia.org/wiki/Rechteckschwingung]

6.2 Messsignale

In der Akustik auch, gibt es verschieden Signale für di Messungen, so wie reiner Ton (Sinus), Impuls, Geräusch oder Sweep. Sie können deterministisch oder random sein.

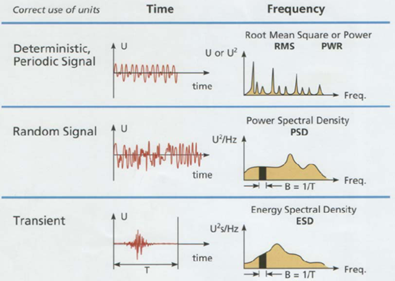
Abbildung. Verschieden Messsignale in der Zeitdomäne und Frequenzdomäne.

[http://www.bksv.com/]

Weißes Rauschen ist ein Rauschen, das durch ein konstantes Leistungsdichtespektrum in einem bestimmten Frequenzbereich beschrieben wird. In der Akustik wird weißes Rauschen als ein stark höhenbetontes Geräusch empfunden. Weißes wird in den Ingenieur- und Naturwissenschaften häufig verwendet, um Störungen in einem sonst idealen Modell abzubilden, z. B. zufällige Störungen in einen Übertragungskanal zu beschreiben. Rosarauschen ist ein gefiltertes Rauschen abgeleitet von weißem Rauschen mit -3 dB/Oktav. Dadurch entsteht ein Signal wo Signal-Rausch-Abstand frequenzunabhängig ist.

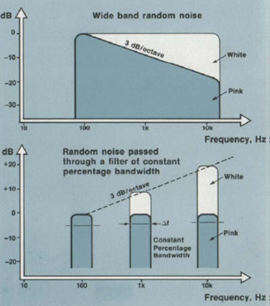
Abbildung. Weißes und Rosarauschen in der Frequenz.

[http://www.bksv.com/]

6.3 Signal-Rausch Abstand

Sowohl bei analoger als auch digitaler Kommunikation ist der Signal-Rausch-Abstand (engl.: signal-to-noise ratio) ein Maß für die Stärke des Signals relativ zum Hintergrund-Rauschen. Das Verhältnis wird oft als S/N oder SNR abgekürzt und normalerweise in Dezibel (dB) angegeben.

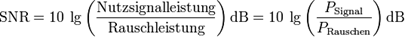
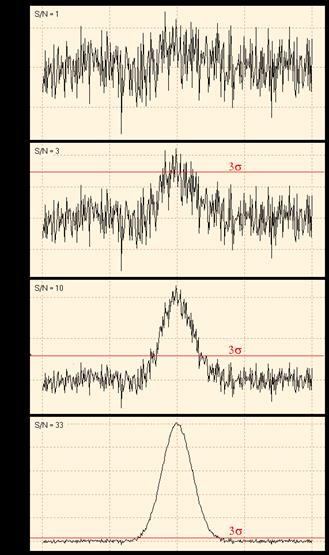
Abbildung. Im obersten Bild ist das Nutzsignal etwa so groß wie das Rauschen des Blindwertes. Hier ist das Signal kaum zu erkennen. Im zweiten Diagramm erreicht das Nutzsignal gerade die Nachweisgrenze (SNR = 3). In den beiden unteren Diagrammen liegt das Nutzsignal bei der zehnfachen bzw. 33-fachen Nachweisgrenze.

[http://www.statistics4u.info/fundstat_germ/ee_detection_limit.html]

In einem digitalen System wird als Quantisierungsrauschen bestimmte Störungen bei der Digitalisierung von Analogsignalen bezeichnet. Da bei der digitalen Repräsentation nur diskrete Werte möglich sind, müssen die abweichenden analogen Messwerte gerundet werden. Der dabei auftretende Fehler - also die Differenz von Originalsignal zu Digitalsignal - wird als Quantisierungsfehler bezeichnet.

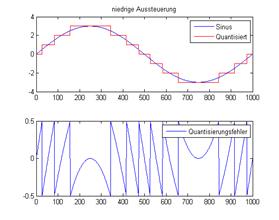
Abbildung. Quantisierungsrauschen.

[http://de.wikipedia.org/wiki/Quantisierungsfehler]

6.4 Schalldruckpegelmesser

Der Schalldruckpegelmesser ist ein Messinstrument um Schalldruckpegel und andere Parameter zu messen. Außer dB-Werte kann es FFT-Analysedurchführen.

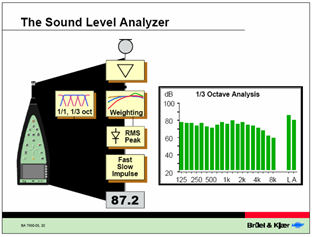
Abbildung. Schalldruckpegelmesser.
[http://www.bksv.com/]

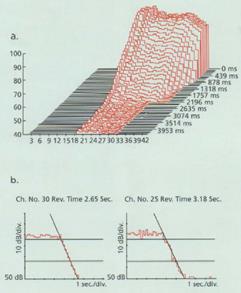
Abbildung. Messergebnisse einer Nachhallzeitmessung.

[http://www.bksv.com/]

Schallfeldgrößen wie Schalldruck, Intensität oder Pegel sind physikalische Größen, objektiv vorhanden und messbar. Kalibration ist aber erforderlich.

Abbildung. Kalibration ist erforderlich.

[http://www.bksv.com/]

Mit einem standardisierten elektrischen Filter lässt sich die Empfindlichkeit eines Schallpegelmessers an das natürliche Lautstärkeempfinden des menschlichen Gehörs angleichen (Frequenz- und Zeitbewertung).

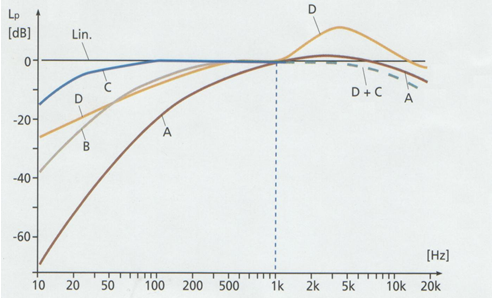
Abbildung. Frequenzbewertungskurven, dB(A) ist das wichtigste.

[http://www.bksv.com/]

Die Messumgebung bestimmt die Ergebnisse auch. Bestimmte Messungen werden im schalltoten Raum durchgeführt, andere vor Ort. In diesem Fall spielen Reflexionen eine wichtige Rolle, welche die Messungen beeinflussen. Auch die physikalische Größe der Schallquelle muss betrachtet werden. Das Nahfeld (a) bezeichnet den unmittelbaren Bereich um die Schallquelle, das von einem ungleichmäßigen Wechsel zwischen Orten mit konstruktiver und destruktiver Interferenz gekennzeichnet ist. Im Gegensatz dazu bezeichnet das Fernfeld (b) einen Bereich, der weit von der Schallquelle entfernt ist. Das Fernfeld besteht aus dem Freifeld (c) und aus dem Diffusfeld (d). Hier werden Messwerte größer sein, da die reflektierte Schallenergie auch mitwirkt.

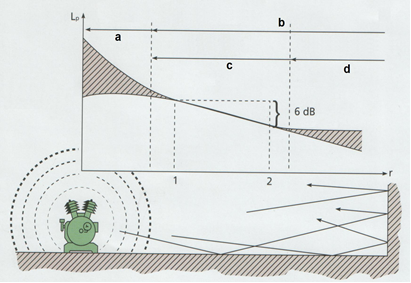
Abbildung. Messumgebungen.

[http://www.bksv.com/]

6.4 Messtechnik

Zu den wichtigsten Methoden gehören Messungen mit Mikrofonen, binaurale Messtechnik, TPA, Modalanalyse und Windkanalmessungen.

Abbildung. Mikrofone im Einsatz.

[AUDI]

Sowohl für Mikrofonmessungen als auch für Beschleunigungsmessungen ist eine Softwareumgebung vorausgesetzt, welche die Signale bearbeitet und darstellt. Zum Beispiel ist dafür das System von HEADAcoustics geeignet. Das SQLab / ArtemiS hat die folgenden Parameter:

Mehrkanal
Analog/Digital
Aufnahme und Auswertung im PC
Modular
Stromversorgung!
Groß
Ohne Ventilator

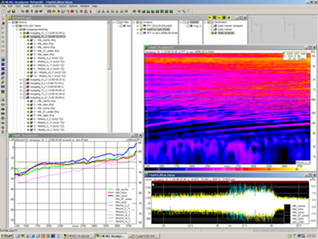
Abbildung. HEADAcoustics ArtemiS.

[AUDI]

Es gibt auch ein portables System, namens Squadriga II:

8-Kanal
Modular
Klein, mobil
Aufnahme und Wiedergabe
Mikrofone und Beschleunigungssensoren
Front-end

SQuadriga_II_perspektive_big

Abbildung. Squadriga II

[AUDI]

Die binaurale Messtechnik arbeitet mit einem Kunstkopf. Messungen und Aufnahmen können sehr realistisch die Wahrnehmung nachbilden und dazu ist ein Kunstkopf mit eingebauten Mikrofonen geeignet.

Abbildung. Binaurale Messtechnik mit Kunstkopf.

[HeadAcoustics]

Transferpfad Analyse (TPA) ist ein weiteres Verfahren. Die verschiedenen Ausbreitungswege zwischen Schallquelle und Ohr nennt man Transferpfade. Die Aufgabe ist es den vibroakustischen Energiefluss von einer oder mehreren Quellen über die relevanten Pfade zum Empfänger aufzudecken und quantitativ zu beschreiben. Das Ziel ist bestimmte Transferpfade unempfindlich zu machen. Die Pfade können reine Körperschallpfade, Luftschallpfade oder eine Mischung aus beidem sein.

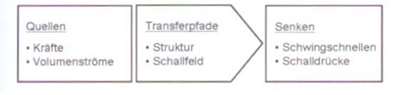
Abbildung. TPA

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

Modalanalyseanalysiert die Moden. Die Modalzerlegung ist ein in der Strukturanalyse angewandtes verfahren. Eine Struktur kann durch ihre Eigenformen (Moden) beschreiben. Das modale Modell kann sowohl analytisch wie auch experimentell ermittelt werden. Im niederfrequenten Bereich der Vibrationen kann die Beschreibung durch ein Modell mit wenigen Moden erfolgen.

Im Windkanal können die aerodynamischen und aeroakustischen Eigenschaften von Objekten vermessen werden. Bei Autos sollen hauptsächlich ein niedriger Luftwiderstand und optimale Auftriebswerte erzielt werden. Bei Audi sind die folgenden Schwerpunkte im Fokus: Kraftstoffverbrauch, Sicherheit, Fahrkomfort und Umweltverträglichkeit, Thermomanagement und Klimatisierung - experimentelle Überprüfung vorausgehender Berechnungen.

Abbildung. Im Windkanal.

[http://www.technik-welten.de/automobil/wie-funktionierts/chassis-karosserie/eis-regen-und-schnee.html]

Luftwiderstand ist nicht nur akustisch gesehen ein wichtiges Problem. Aufgabe des Motors ist die Wirkung gegen Reibkräfte, und vor allem Luftwiderstand. Parametersind hier Luftdichte (ρ), Oberfläche (A), Geschwindigkeit (v), Strömungswiderstandskoeffizient (C_w):

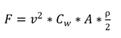
C_w ist bei einer Platte ca. 1, bei einer Kugel ca. 0,3-0,5, beim "Tropfenform" gegen 0,2-0,05.

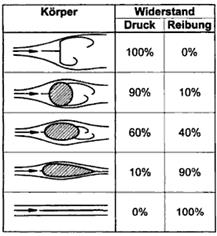
Abbildung. Körperform beeinflusst Druck und Reibung.

[http://de.wikipedia.org/wiki/Str%C3%B6mungswiderstand]

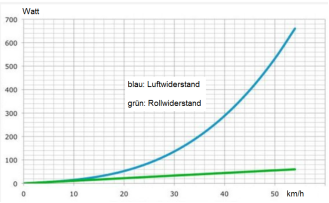
Abbildung. Geschwindigkeit beeinflusst Roll- und Luftwiderstand unterschiedlich.

[http://de.wikipedia.org/wiki/Str%C3%B6mungswiderstand]

*****************************************************************************************************************************************

7. Schwingungen im Fahrzeug

7.1 Kundenerwartungen und Entwicklung

In den letzten Jahrzehnten sind sowohl Kundenerwartungen als auch Entwicklungen exponentiell angestiegen. Das betreibt ständige Entwicklung auf dem Gebiet der Fahrzeugakustik.

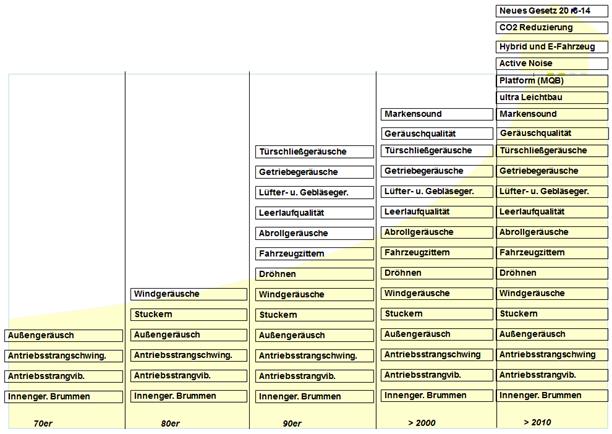
Abbildung. Kundenerwartungen.

[AUDI]

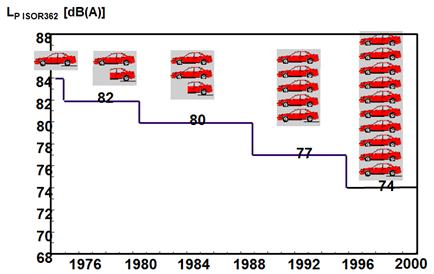
Abbildung. Geräuschentwicklung.

[AUDI]

Bald wird es nicht nur eine obere Grenze, sondern auch eine untere Grenze vorgeschrieben (wegen e-Antriebe, die zu leise sind).

Die Aufgaben der Fahrzeugakustik stellen oft Zielkonflikte dar (Komfort vs. Sportlichkeit und/oder Sicherheit).

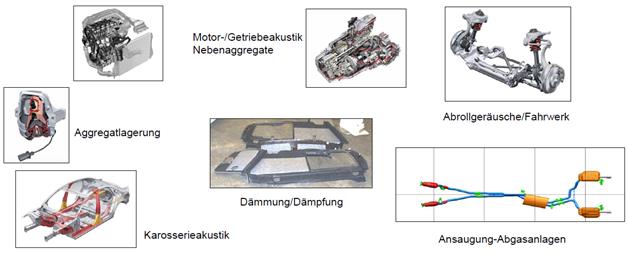
Abbildung. Felder der Fahrzeugakustikentwicklung.

[AUDI]

7.2 Vibroakustische Fahrzeugeigenschaften

Über die Kontaktflächen des Insassen zum Fahrzeug werden schwingende Oberflächen als Vibrationen empfunden (Sitz, Lenkrad, Bodenbereich). Als Schwingungsquellen sind folgende vier Bereiche wichtig:

Antriebseinheit aus Verbrennungsmotor und Nebenaggregaten,
Interaktion zwischen Fahrbahn und Rad,
Aerodynamische Umströmung (bei Bewegung),
Mechatronische Aktoren.

Vibrationen können ebenfalls als Körperschall im Infraschallbereich angesehen werden, die über die Kontaktstellen des Körpers taktil wahrgenommen werden. Die Schwingungen im fühlbaren und hörbaren Frequenzbereich werden unter dem Begriff "Vibroakustik" zusammengefasst. Vibroakustik umfasst "noise, vibration and harshness (NVH)".

7.3 Subjektive Beurteilung

Steigerung des Komforts ist oft das Vermeiden oder Senken des Diskomforts. Subjektive Bewertung des vibroakustischen Komforts kann zwei Arten erfolgen:

Indirekt, wo die Auswirkungen des Diskomforts auf die Konzentrationsfähigkeit des Probanden erfassen werden. Dazu werden den Probanden Aufgaben gestellt und deren Lösung bewertet. Das erfordert hohen Aufwand.
Direkt, wo der Beurteiler gezielt nach seiner Empfindung befragt wird. Nachteilig ist, dass die Urteile nicht in einer vergleichbaren Form vorliegen.

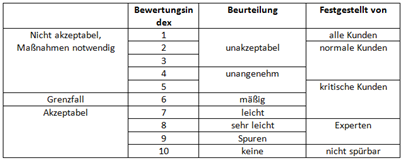
Abbildung. Beurteilungsindex.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

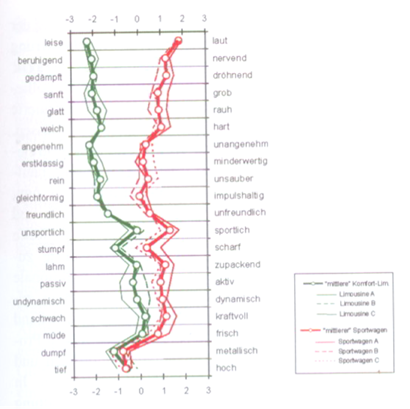
Abbildung. Semantische Profile für das Innengeräusch in Limo und Sportwagen. Ein ähnliches Diagramm kann auch kreisförmig dargestellt werden (so genannte "akustische Spinne").

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

7.4 Fahrkomfort

Der subjektiv empfundene Fahrkomfort (ganz besonders bei PKWs) spielt eine wichtige Rolle. Dazu zählt man auch Schallemission und Schwingungseigenschaften. Komfortpunkte sind

die Kontaktfläche des Insassen zum Sitz,
Fußaufstandsflächen und
der Kontakt der Hand zum Lenkrad.

Hier müssen Schwankungspegel niedrig sein.

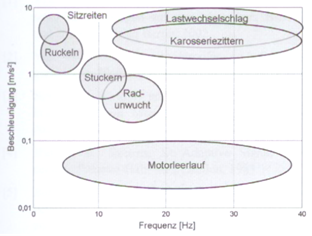
Abbildung. Beschleunigung von Schwingungen im Auto.
[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

Schwingungen können…

sowohl in den drei translatorischen Freihetsgraden

(x, y, z ; Längs-, Quer- und Vertikaldynamik)

…als auch in den drei zugehörigen rotatorischen Freihetsgraden

(Φ, ϑ, t; Nicken, Wanken und Gieren) auftreten.

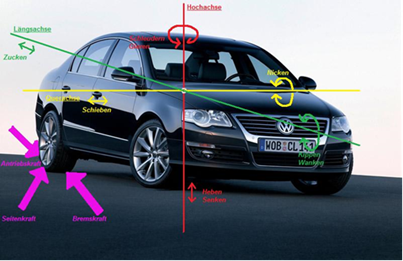
Abbildung. Koordinaten.

[http://www.bonk-kfz.de/fahrzeugfederung/]

7.5 Modellbildung

Modellbildung heißt, die Realität soweit aufgrund der Problemstellung zulässig zu vereinfachen, ohne die interessierenden Sachverhalte unzulässig zu verfälschen.

empirisches (black-box) Modell:
der Aufbau des Systems noch unbekannt ist,
hat Eingänge und Ausgänge, aber das Innenleben ist unbekannt oder unwichtig,
die Reaktion des Systems kann mit verschiedenen Eingangssignalen getestet werden,
mit einer großen Zahl lässt sich eine Hypothese über den Zusammenhang bilden.
physikalisch begründetes Modell (white-box):
der Zusammenhang zwischen Eingang und Ausgang aufgrund der Kenntnis von den inneren Zusammenhängen des Systems analytisch herleiten.
Beispiel ist eine FEM-Analyse.

Ein gutes Beispiel ist das "Zweispurmodell" eines Autos. Hier werden nur zwei Spuren in Betracht gezogen.

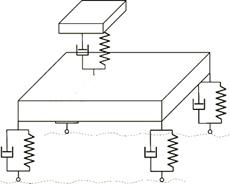
Abbildung. Zweispurmodell eines Autos, 4 Räder und Sitz.

[AUDI]

Schwingungen sind oft in vier Gruppen aufgeteilt:

Bei freien Schwingungen (Eigenschwingungen)
wird das System ausgehend von einem Anfangszustand sich selbst überlassen und kommt nach einem Einschwingvorgang zur Ruhe.
Das System wird nach einer einmaligen Anregung sich selbst überlassen und kommt durch die Dämpfung zur Ruhe (z.B. geschwindigkeitsproportionale Reibung).
Die Frequenz wird durch die Systemparameter bestimmt.
Beispiele sind: Einmassenschwinger, ungeffester Zweimassenschwinger, gekoppelte Systeme.
Bei erzwungenen Schwingungen
schreiben äußere Kräfte die Energiezufuhr und damit die Frequenz vor.
Dem System wird permanent Schwingungsenergie zugeführt, und wird die Schwingung erhalten.
Es kann auch ein Einmassenschwinger oder Zweimassenschwinger sein.
Selbsterregte Schwingungen takten die notwendige Energiezufuhr selbst.
Die Frequenz ist sowohl durch Systemparameter als auch durch die Anregung bestimmt.
Es sind freie Schwingungen, welche nicht durch die Dämpfung abklingen, sondern durch eine Quelle Energie zugeführt bekommen.
Hier bestimmt das System selbst die Frequenz der Energiezufuhr.
Die erste Gruppe solcher Schwingungen sind wo die Ursache in den tribologischen Parametern des Reibkontaktes haben (Kupplungsrupfen, Kontaktstellengeräusche).
In der anderen Gruppe wird das Schwingungsverhalten durch die geometrischen und dynamischen Eigenschaften des mechanischen Systems bestimmt (Bremsenquitschen).
Bei parametererregten Schwingungen
sind mehrere Koeffizienten in der Differentialgleichung nicht konstant, sondern ändern sich periodisch.
Die Frequenz wird von außen gesteuert.

7.6 Fahrbahnerregte Schwingungen

Sie werden durch die Unebenheitensanregung der Räder beim Überfahren der Fahrbahn angeregt.

- Zweispurmodelle sind erforderlich, um die von der Fahrbahnoberfläche ausgehenden Anregungen an allen vier Rädern zu erfassen.

- Bei einem geradlinigen Fahrweg und korrelierter Anregung der zwei parallelen Fahrspuren kann die Dynamik um die Längsachse (Wanken) vernachlässigt werden (Einspurmodell).

- Vernachlässigt man noch die Dynamik um die Querachse (Nicken), ist es ein Viertelmodell.

Für den fahrbahnerregten Schwingungskomfort ist die Dynamik in Richtung "auf" (Vertikaldynamik mit einem Einspurmodell) relevant. Es muss immer der Zielkonflikt zwischen Fahrkomfort und Fahrsicherheit/Fahrdynamik aufgelöst werden. Es werden auch semi-aktive und vollaktive Fahrwerke eingesetzt um den Zielkonflikt zu lösen. Ein weiteres Komfortkriterium ist das Systemverhalten beim Überfahren von Fahrbahnstufen. Idealisiert kann man die Anregung im Zeitbereich als Sprungfunktion betrachten. Harmonische, deterministische Unebenheitsanregungen sind selten. Vielmehr geht es um mehr oder weniger zufällig verteilte unregelmäßige Unebenheiten (stochastisches Modell). Der tieffrequente Schwingungskomfort beim System Sitz-Mensch kann mit einem Viertelmodell beschrieben werden.

Hier sind Frequenzen zwischen 1-4 Hz zu betrachten.
Bei ca. 3 Hz gibt es die eigentliche Sitzresonanz, und bei 7-8 Hz sind die Körperresonanzen zu finden.

Karosseriezittern tritt vor allem bei Fahrzeugen mit großer Dachöffnung (Cabrios) oder Hecköffnung (Kombi) auf. Beim Motorstuckern geht es um eine Koppelschwingung zwischen dem elastische gelagerten Motor-Getriebe-Verband und dem Aufbau. Die Anregung erfolgt durch symmetrische Fahrbahnunebenheiten auf beiden Spuren (auf der Autobahn häufig). Hier sind Videos zu finden: http://www.youtube.com/watch?v=9A8dq0hzdLs, http://www.youtube.com/watch?v=ED7iOqY-w7k

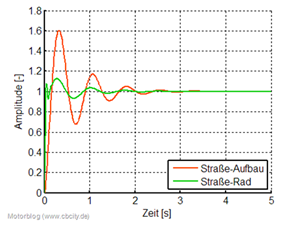
Abbildung. Schwingungen in der Zeit und in der Frequenz.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

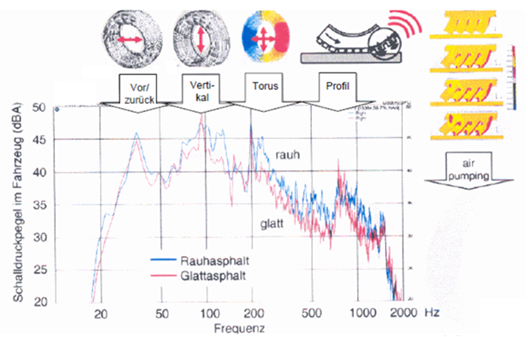
Abbildung. Schwingungen beim Rad.

[AUDI]

7.7 Raderregte Schwingungen

Schwingungen, die infolge mangelnder Gleichförmigkeit des Systems Rad/Reifen entstehen (insbesondere bei höheren Geschwindigkeiten). Ursache dafür können sein: Unwucht, Steifigkeitsschwankungen, Rundlauffehler. Hierher zählt man auch Anfahr- und Bremsstempeln. Damit führt das Rad keine reine Vertikalschwingung sondern bewegt sich auf einer elliptischen Bahnkurve (dabei spielt Reifenfülldruck eine wichtige Rolle). Das Phänomen, das vor allem bei Eingelenkern mit großem Federweg auftritt, ist das so genannte Bremsstempeln: http://www.youtube.com/watch?v=iIv8cKRyq3s

7.8 Motorerregte Schwingungen

Für motorerregte Schwingungen sind Beispiele:

Leerlaufschwingungen des Motors,
Start-Stop-Schwingungen,
Reibschwingungen bei schlupfender Kupplung und
Lastwechselschwingungen.

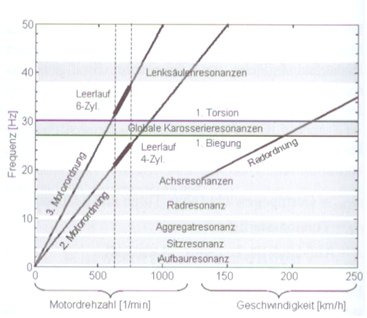
Abbildung. Ordnungsanalyse (siehe später) von Resonanzen.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

7.9 Karosserieschwingungen (Strukturdynamik)

Durch die Karosserie werden alle Teilsysteme des Fahrzeugs miteinander gekoppelt. Das dynamische Verhalten der Karosserie wird durch die Lage der globalen Eigenfrequenzen und durch die Ausprägung der Schwingformen charakterisiert. Zu geringe statische Karosseriesteifigkeiten beeinflussen die Fahrdynamik negativ, können zu Klapper- und Knarzgeräusche führen und haben auch die Folge, dass sich Türen, Klappen, nicht einwandfrei öffnen und schließen lassen. Für Schwingungen, deren Frequenz über von 2 bis 4 Hz liegen, kann die Karosserie nicht mehr als nur elastisch angesehen werden. Die globalen Eigenformen sind für das Schwingungsverhalten und die lokalen Schwingformen für die Körperschalleinleitung und Übertragung relevant. In der Entwicklung ist es notwendig, die Auswirkungen verschiedener Zielsysteme von Eigenfrequenzkonfigurationen der bestimmenden globalen Eigenformen auf den Schwingungskomfort des Fahrzeuges darzustellen.

7.10 Schwingungsminderung

Es gibt drei verschiedene Arten von Schwingungsminderung:

Passive Maßnahmen beeinflussen das Übertragungsverhalten des Transferpfades durch Veränderungen von Bauteilparametern (ohne zusätzliche Energie).
Semi-aktive Maßnahmen beeinflussen die Übertragungsfunktionen der Transferpfade jedoch abhängig vom Betriebszustand. Diese wird durch aktiv steuerbare oder regelbare Elemente durchgeführt (mit Hilfe von Hilfsenergie).
Bei voll-aktiven Maßnahmen erfolgt die Beeinflussung über die Aufprägung von zusätzlichen Kompensationskräften (mit erheblicher Energie).

Abbildung. Schwingungsminderungsmethoden.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

Bei passiven Maßnahmen sollen die Anregungen sollten vor der Bekämpfung erledigt werden. Wenn nicht: Resonanzfrequenzen sind zu verschieben um ungünstige Kombinationen zu vermeiden. Die wichtigste passive Maßnahme ist

die Isolation (durch elastische Lagerung) und
die Tilgung von resonanzhaften Phänomenen durch Applizieren eines abgestimmten zusätzlichen Schwingungssystems auf der zu beruhigenden Masse.

Alle Methoden zeigen Wirkung nur in bestimmten Frequenzbereichen. Außerhalb der Bereiche kann man sogar mit einer Verstärkung rechnen.

Isolation (Entkoppelung)

Die Schallquelle muss entweder schwingungstechnisch von der Umgebung getrennt, oder der Empfänger von den Schwingungen isoliert werden. Bei der einfach elastischen Lagerung erfolgt die Trennung mittels EINER zwischengeschalteten Lagerebene. Bei doppelt elastischer Lagerung wird die Quelle durch eine Zwischenmasse und ZWEI federnde Lagerelemente isoliert. Widersprüchliche Anforderungen sind zu erfüllen:

Ausreichende Steifigkeit und damit kleine Federwege zum Tragen der statischen Last,
hohe Dämpfung von niederfrequenten Schwingungen um die Amplituden im Resonanzfall zu begrenzen,
Gute Isolation von höherfrequenten akustischen Einträgen und damit geringe Steifigkeit und niedrige Dämpfung.

Es werden Federelemente mit Dämpferelementen kombiniert. Elastische Federelemente sind Stahlfedern oder Luftfedern (linear). Schwingungsdämpfer sind nicht linear (hydraulischer Teleskopdämpfer, Luftfederdämpfer).

Dämpfung

Dämpfung ist immer die Umwandlung von kinetischer Energie in Wärmeenergie (Dissipation). Es gibt folgende Varianten von Dämpfung:

Materialdämpfung auf mikroskopischer Ebene durch innere Reibung bzw. Plastizität eines Festkörpers,
Viskose Dämpfung durch Scherkräfte auf mikroskopischer Ebene in Flüssigkeiten oder Gasen,
Reibungsdämpfung auf makroskopischer Ebene durch Kräfte an der Grenzfläche zwischen Reibpartnern,
Abstrahldämpfung bei schwingenden Oberflächen.

Dämmung heißt dass Schall reflektiert wird und so nicht weitergeleitet.

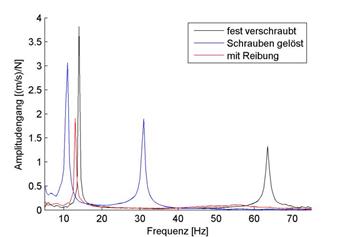
Abbildung. Resonanzen bei Schwingungen mit und ohne Schrauben.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

Tilgung

Tilgung ist die Kompensation der Wirkung von translatorischen Erregerkräften oder rotatorischen Erregermomenten durch entgegengesetzt gerichtete Massenkräfte oder -momente. Bei passiven Tilgern wird diese Gegenkraft durch ein Feder-Masse-System erzeugt. Bei aktiven Systemen werden die Kräfte von aktiv angesteuerten Aktuatoren aufgebracht. Tilgung ist die Beruhigung einer Teilstruktur eines Systems durch Umleitung der Schwingungsenergie auf eine andere Teilstruktur. In der Umgebung der Tilgungsfrequenz werden Amplituden erheblich reduziert, gleichzeitig aber zwei neue Schwingmoden mit vergrößerten Amplituden entstehen.

Abbildung. Schwingungstilger mit elastischem Anschlagpuffer.

[http://www.contitech.de/pages/produkte/schwingungstechnik/antriebsstrang/schwingungstilger_de.html]

[http://www.wegu.de/OverloadProtectionVibrationAbsorbers.aspx]

7.11 Aktive Kompensation

Aktive Maßnahmen sind Teil der "Akustik 2.0". Aktive Kompensation wurde erstmal zur Unterdrückung von unerwünschtem Luftschall unternommen. Heute wird es auch für Körperschall und Schwingungen eingesetzt. Das Prinzip beruht auf der Interferenz eines unerwünschten Störsignals mit einem erzeugten Kompensationssignal, welches geeignet ist, das Störsignal zu eliminieren. Beim Steuerungsansatz (Feed Forward)

wird die Störgröße erfasst und
daraus ein Kompensationssignal abgeleitet.

Beim Regelungsansatz (Feedback)

wird das Kompensationssignal aus der
rückgeführten Regelgröße berechnet.
Für eine messbare Störgröße müssen Sensoren installiert werden.
Hierher zählt aktive Lagerung, AVC, ANC (siehe später), usw.

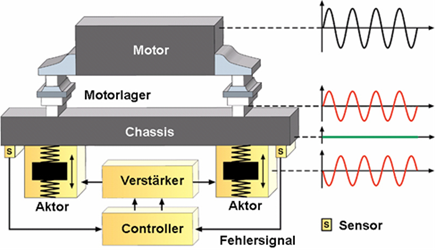
Abbildung. Active Vibration Control/Cancelling (AVC).

[http://www.contitech-megi.de/pages/current/press/2008/080527_schwingung/presse_en.html

*************************************************************************************************

8. Geräusche und Geräuschminderung im Fahrzeug

8.1 Geräusche im Fahrzeug

Geräusche im Fahrzeug können verschiedene Gründe haben. Sie können innen entstehen und nach außen abgestrahlt werden (siehe rot in der Abbildung), oder umgekehrt (blau). Vibrationen unter 30 Hz können sowohl als Vibration und manchmal auch als sekundärer Luftschall wahrgenommen werden.

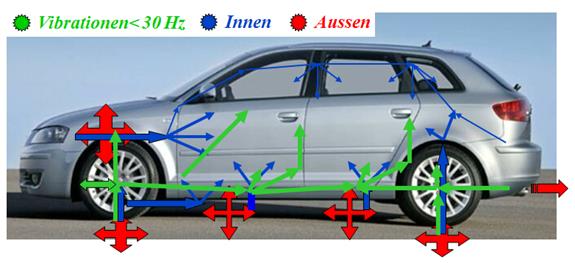
Abbildung. Geräusche im und um das Fahrzeug.

[AUDI]

Die folgenden Gebiete sind für die Geräuschaufteilung wichtig:

Ladungswechselgeräusch
Reifen-Fahrbahngeräusch
Stör- und Betätigungsgeräusch
Türbetätigungsgeräusch
Audio (Autohifi)

8.2 Ladungswechselgeräusch

Es umfängt vom Ansaug- und Abgassystem abgestrahlten Geräuschanteilen. Sie können durch periodische Arbeitsprozesse verursacht werden oder durch kontinuierlichen turbulenten Durchströmung der Luft und Gas führenden Bauteile. Das Strömungsgeräusch ist bei niedrigen Drehzahlen und hoher Last von Bedeutung. Bei höheren Drehzahlen dominieren immer mehr die mechanischen Geräusche. Das Ansaugsystem's Aufgabe ist Frischluft für die Verbrennung zu führen. Der Luftfilter dient auch zur Geräuschdämpfung (Dieselmotor mehr problematisch). Die Abgasanlage ist für Abführung und Reinigung der heißen Abgase, Dämpfung des Abgasgeräusches (und Sound Design) da. Es ist auch möglich "Lautsprecher" in das Abgassystem zu installieren, wie z.B. das System "Sound Actor" von Audi, welches es ermöglicht den sportlichen Charakter des Autos zu erhöhen (ein V6 Motor kann wie ein V8 klingen). Die akustische Auslegung ist schwierig da hier Zielkonflikte vorliegen.

8.3 Reifen-Fahrbahngeräusch

Reifen stehen für die Sicherheit. Breitere Reifen sind besser, aber strahlen mehr Schall ab. Luftreifen reduzieren das Rollgeräusch sehr viel. Reifenprofil und Laufstreifenmischung sind hier sehr wichtig. Reduzierung des Rollgeräusches heißt die Abstrahlung der Strukturschwingungen des Reifens zu vermindern. Reifenhersteller verwenden unterschiedlich lange Blöcke am Reifen um eine tonale Anregung zu vermeiden und um die Schallenergie zu verteilen. Beim rollenden Reifen ist im Bereich der Bodenaufstandsfläche eine Kompression der Luft in den Profilrillen zu erwarten (AirPumping). Je glatter und dichter die Fahrbahnoberfläche ist, desto größer ist die Möglichkeit zum Lufteinschluss (Zischgeräusch). Hier spielt auch die Fahrbahntextur eine wichtige Rolle. Das Rollgeräusch muss nicht nur im Fahrzeug sondern auch außerhalb des Fahrzeugs untersucht werden.

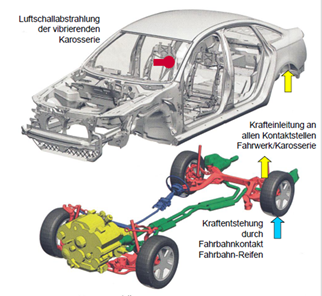
Abbildung. Karosserie als leitendes Element für Vibrationen.

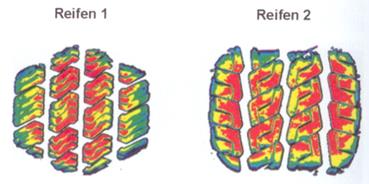
Abbildung: Reifen 1: geräuschempfindliche Reifenmitte, Reifen 2: optimale Verteilung.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

8.4 Stör- und Betätigungsgeräusch

Fahrgeräusche verursachte Geräuschpegel im Innenraum werden geringer so treten Nebengeräusche verstärkt auf. Wird ein Geräusch einmal wahrgenommen, so bleibt es im Vordergrund. Auftretenshäufigkeit, Intensität, Lokalisierbarkeit sind wichtig und werden sehr subjektive beurteilt.

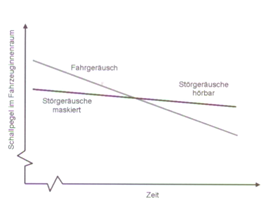
Abbildung. Als Fahrgeräusch immer niedriger wird im Fahrzeug, werden vorher maskierte Geräusche hörbar.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

Mechatronische Geräusche werden durch Systeme verursacht, wo ein mechanisches Hauptsystem arbeitet. Hier werden elektrische Sensoren verwendet, welche auf mechanische (hydraulische) Systeme wirken.
Elektrische Stellmotoren, Lüfter und Gebläse, Klimaanlage, Lenkungssystem, Bremssystem usw.
Kontaktstellengeräusche aufgrund von Relativbewegungen von Bauteilen werden als Störgeräusche sehr unangenehm wahrgenommen. Solche Geräusche sind instationär und treten zufällig auf. Eine subjektive Beurteilung ist oft genügend. Lange Impulse reduzieren den Frequenzbereich, erhöhen aber die Amplituden.
Klapper-, Knarz- und Quitschgeräusche.
Zufällige und kontinuierliche Störgeräusche, welche nicht einzelnen Ereignissen zugeordnet werden können, sind noch lästiger. Die Ursache ist nicht immer bekannt und kann auch nicht beeinflusst werden. Die Ursache dafür sind stationäre Schwingungen im Fahrzeug, durch unebenen Straßenbelag oder durch Audiobeschallung erregt.

8.5 Türbetätigungsgeräusch

Das Geräusch beim Öffnen und Schließen der Türe ist ein wichtiges Erlebnis aus der man oft Rückschlüsse auf die Qualität des gesamten Fahrzeuges zieht. Öffnungsgeräusche werden von 50-54 dB(A) und Schließgeräusche von 58-62 dB(A) als richtig eingestuft. Anstrebenswert ist auch ein eher dunkles Klangbild ohne Klicken. Der größte Teil des Geräusches entsteht im Schloss (Körperschall), Tür und Karosserie werden schwingen und indirekter Luftschall wird abgestrahlt.

Abbildung. Zeitablauf eines Türbetätigungsgeräusches.

[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

8.6 Audio

Die Wiedergabequalität von Audioquellen stellt immer einen Beanstandungspunkt dar. Insbesondere die Wechselwirkung der Lautsprecher mit den umgebenden Interieur-Teilen ist kritisch. So kann der Lautsprecher nicht nur die Membran sondern auch das Verkleidungsteil bewegen. Dies führt zu einem akustischen Kurzschluss und Verzerrungen. Eine weitere Frage ist die Anzahl (Kanäle) der Lautsprecher.

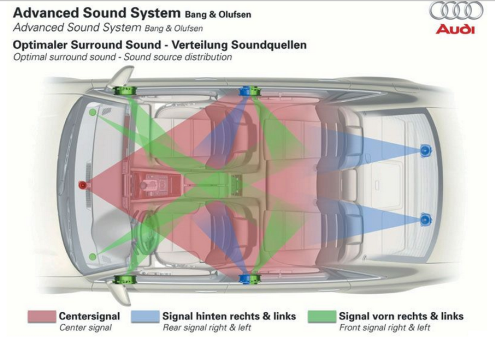
Abbildung. B&O Sound System bei Audi.

[AUDI]

[http://fourtitude.com/news/Audi_News_1/the-audi-a8-bang-and-olufsen-advanced-sound-system-in-depth/]

8.7 ANC - Active Noise Control / Cancellation

Unter Antischall (auch "aktive Lärmkompensation", englisch Active Noise Reduction [ANR] oder Active Noise Cancellation [ANC]) versteht man umgangssprachlich Schall, der künstlich erzeugt wird, um mittels destruktiver Interferenz Schall auszulöschen. Dazu wird die Erzeugung eines Signals angestrebt, das dem des störenden Schalls mit entgegengesetzter Polarität exakt entspricht. Mit ANC im Fahrzeug kann man drehzahlabhängige Motorgeräusche auslöschen, wenn Mikrofone im Motorraum platziert sind.

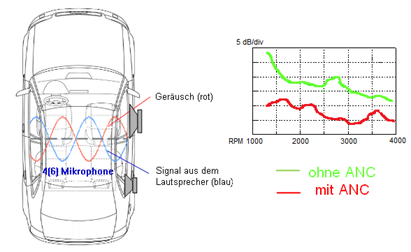
Abbildung. ANC kann durch destruktive Interferenz Geräuschpegel bis zu 15-20 dB reduzieren.

[AUDI]

Weitere interessante B&O Demo Videos sind hier zu finden: http://www.youtube.com/watch?v=eAnF2YDZAA0, http://www.youtube.com/watch?v=iZervJ3sZv0, http://www.youtube.com/watch?v=2mwFyUNV0x4

Der "Sound Actor" von Audi ist ein System u Motorgeräusche im Inneren zu erhöhen. Es besteht aus einem vibrierenden Teil welcher sie Frontscheibe als Membran bewegt je nachdem wie der Fahrer das wünscht. Es kann auch einen Teil in der Abgasanlage haben. Beide werden aktiv über CAN-BUS kontrolliert.

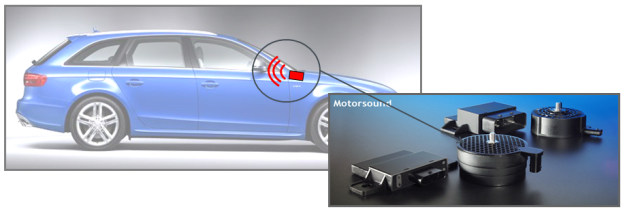
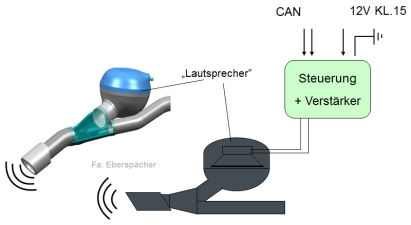
Abbildung. Sound Actor bei Audi.

[AUDI]

8.8 Audi Sound Videos

Um noch mehr Aufgaben und Gebiete der Akustik zu erforschen, sind folgende "Audi TV" Videos zu empfehlen:

https://www.youtube.com/watch?v=R63Ybfk84rs

https://www.youtube.com/watch?v=QsD7RH0iDxQ

https://www.youtube.com/watch?v=E6w2alhbIZc

***********************************************************************************************************************************

9. Grundlagen numerischer Methoden

9.1 Hintergrund

Hier werden die Grundlagen und der mathematischer Hintergrund für die numerischen Methoden eingeführt. Dieses erfordert die Kenntnisse in Differentialberechnungen. Um die numerischen Methoden und Anwendungen kennenzulernen, kann dieser Kapitel übersprungen werden.

Wie schon gesehen, ist Schall kleine und schnelle Veränderung des Luftdrucks um den Mittelwert. Mittelwert ist 10⁵ Pa (Atm), die Veränderungen etwa 10^-5 - 10². Für die Berechnungen brauchen wie die akustischen Variablen: Druck (p), Teilchengeschwindigkeit (v₀), Dichte (ρ), Temperatur (T). Ausbreitungsgeschwindigkeit (Schallgeschwindigkeit) ist im Medium konstant (c=340 m/s ≠ v₀). Teilchengeschwindigkeit ist kleiner als c.

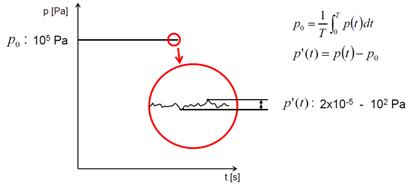
Abbildung. Schall ist kleine und schnelle Veränderung des Luftdrucks um den Mittelwert.

[AUDI]

9.2 Akustische Variabel

Um die Berechnungen zu machen brauchen wir die folgenden Voraussetzungen:

Luft ist ein Kontinuum: homogen, ohne Dämpfung.
Die thermischen Veränderungen sind reversibel und adiabatisch.
Nur kleine Amplituden kommen vor.
Das Medium bewegt sich nicht, nur der Schwingungszustand breitet sich vor (v₀=0).

9.3 Mathematisches Modell

Die Interpretation ist wie folgend. Es gibt Veränderungen

als Funktion des Ortes in einem Zeitpunkt,
als Funktion der Zeit an einem Ort,
und diese sind proportional (c²),
wobei λ=c/f.

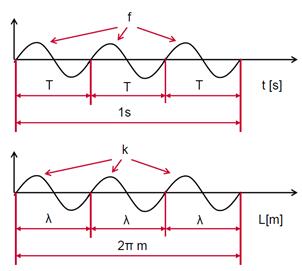
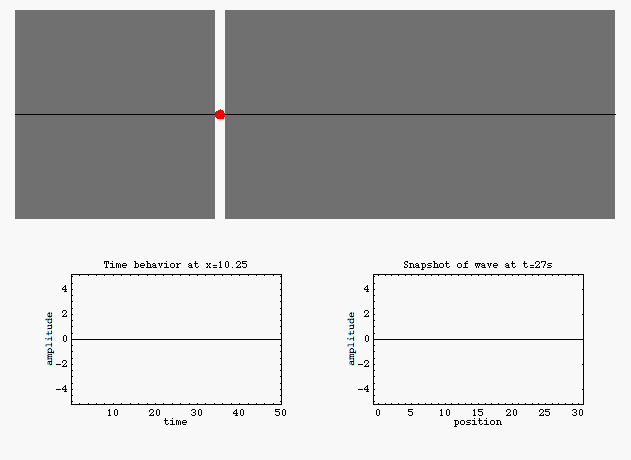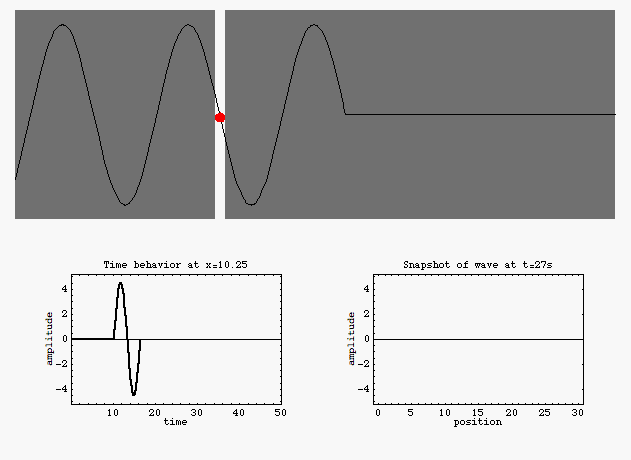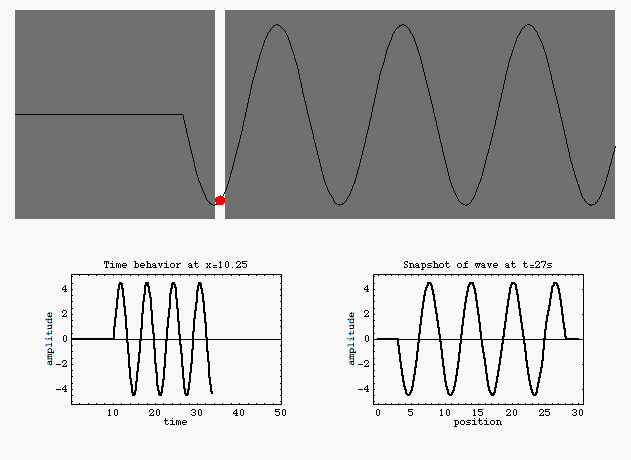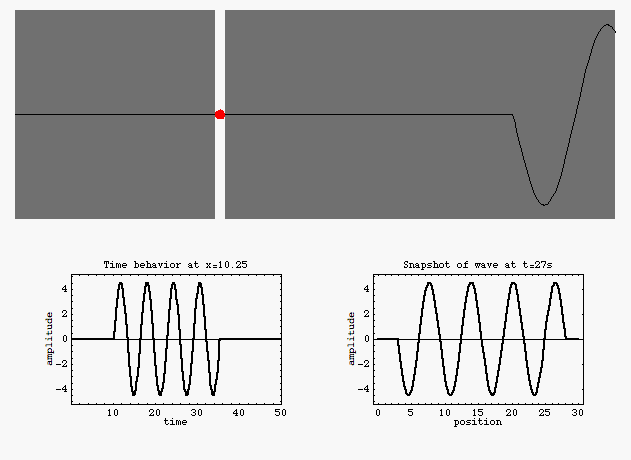
Abbildung. Interpretation der Wellengleichung: es gibt die selben Veränderungen als Funktion des Ortes in einem Zeitpunkt und als Funktion der Zeit an einem Ort.

[http://www.acs.psu.edu/drussell/demos.html]

9.4 Die Wellengleichung

Die Wellengleichung beschreibt dass die die Beschleunigung eines kleinen Abschnitts einer schwingenden Saite ist der mittleren Auslenkung benachbarter Abschnitte proportional. Die Saiten (oder andere physikalische Systeme in denen wellen auftreten) bewegen sich wellenförmig. Eine Saite ist ein einfaches Beispiel: 1D Bewegung in einer Ebene. Es ist eine "unendlich dünne" Linie, und die Lösung des Problems ist relativ einfach. Eine Saite ist ein Kontinuum, eine Line aus unendlich vielen Punkten. Ein Modell kann sie beschreiben als sehr viele dicht gepackte Massenpunkte, die mechanisch durch "Federn" verbunden sind.

Das Hooke'sche Gesetz sagt: Die Längenänderung einer (mechanischen) Feder ist der Kraft, die auf sie ausgeübt wird, proportional. Eine schwingende Saite hat zu jedem Zeitpunkt die Form einer Sinuskurve (im Raum). Außerdem, die Auslenkung der Schwingung folgt ebenfalls einer Sinuskurve (in der Zeit). Die Saite auf und abschwingend dieselbe Bewegung fortwährend wiederholt. Die Periode - die Zeit zwischen Wiederholungen - ist 2π/c. Die Situation kann auch mit den Moden beschreiben lassen, wobei gleichzeitig mehrere Sinuswellen (Moden) auf der Saite schwingen. Die Auslenkung ist mit einem zeitabhängigen Faktor - der sich ebenfalls sinusförmig sich ändert - multipliziert. In allen Fällen sind die Enden der Saite fix (fest eingespannt). Je mehr Wellenberge und Wellentäler (Knoten), desto schneller die Schwingung.

Die Wellengleichung enthält den Begriff "partielle Ableitung". Wenn eine Funktion (u ist jetzt die Amplitude, die Auslenkung) nicht nur vom Ort x sondern auch von der Zeit t abhängt, kann man die Ableitung nach der Zeit und/oder nach dem Ort ausrechnen. Zu jedem Zeitpunkt kann man du/dx ausrechnen. Das ist der Anstieg der Welle an diesem Ort und zu dieser Zeit. Man kann auch den Ort festhalten und du/dt ausrechnen, welche dann die Geschwindigkeit ist. Die kleine Veränderung du in den beiden Fällen kann und ist oft unterschiedlich. Dafür ist das Symbol ∂ da um es zu zeigen, dass es hier um Veränderungen hinsichtlich verschiedener Variablen geht.

Die Kurvenform der Saite hängt vom Ort und von der Zeit ab. Newton's Gesetz (f=ma) sagt dass die Beschleunigung (die zweite Ableitung nach der Zeit) eines kleinen Segments zu der Kraft proportional ist. Die Kraft kommt von Nachbarsegmenten ausgeübt, und Nachbar bedeutet hier eine kleine Veränderung im Ort. Die Wellengleichung sieht am Ende so aus:

Hier ist u(x,t) die senkrechte Position (Auslenkung) am Ort x zur Zeit t, und c ist Ausbreitungsgeschwindigkeit. Es ist eine lineare partielle Differentialgleichung. Links steht Beschleunigung, während die zweite Ableitung nach dem Ort entspricht der Kraft. Da alle Störungen als klein angenommen werden, kann die Linearität erhalten bleiben und so lässt sich die Gleichung relativ einfach zu lösen. Die Kraft auf ein Stück Saite kann durch eine lineare Kombination kleiner Auslenkungen der Nachbarelemente genähert werden. Jede Lösung ist eine Überlagerung (Superposition) von zwei Wellen: eine die sich nach links, und eine die sich nach rechts wandert. Die stehenden Wellen sind eine Kombination von gleich geformten Wellen. Wenn es um 3D Lösungen geht, sieht die Gleichung so aus:

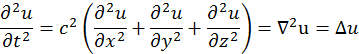
Die Laplace'sche Verschiebung stellt die mittlere Auslenkungsdifferenz zwischen u am untersuchten Ort und seinem Wert an Nachbarorten dar. In zwei Dimensionen lassen wir z weg, und Lösungen können ebene Formen sein. Die einfachsten Schwingungsmuster sind die Eigenmoden. Alle Wellen kann man durch Überlagerung von Eigenmoden erzeugen. Die Frequenzen der Eigenmoden stellen die natürlichen Schwingungsfrequenzen dar. Bei rechteckigen Bereichen sind diese trigonometrischen Funktionen, bei einem Kreis jedoch Bessel-Funktionen. Im Falle eines beweglichen Mediums muss die Navier-Stokes-Gleichung angewendet werden.

***********************************************************************************************************************

10. Numerische Methoden

10.1 Freiheitsgrade

Die folgenden Methoden werden später näher angegangen: MKS, SEA, FEM, BEM, PML, AML, CFD, TMM und Ray-Tracing

Mit Freiheitsgrad (Degrees-of-freedom, DOF) wird die Zahl der voneinander unabhängigen (und in diesem Sinne "frei wählbaren") Bewegungsmöglichkeiten eines Systems bezeichnet. Ein starrer Körper im Raum hat demnach den Freiheitsgrad 6, denn man kann den Körper in drei voneinander unabhängige Richtungen bewegen und in drei voneinander unabhängigen Ebenen drehen. Ein starrer Körper ohne Bindungen hat demnach drei Translationsfreiheitsgrade und drei Rotationsfreiheitsgrade. Ein elastisches Kontinuum, z.B. Luft hat unendliche DOF. In FEM (siehe später) ist N die Anzahl der Knoten. Da jede Knote 6 DOF hat, und ein Modell der Karosserie kann bis zu N=1,5 Millionen Knoten haben ist die Gesamtzahl etwa DOF=9 Millionen! Wenn ein Knoten gleichzeitig mechanisch und akustisch sind ist DOF=7.

Es ist immer wichtig, dass im Falle von kleinen Auslenkungen und kleinen Druckveränderungen betrachten wir das System linear, wo Ausgang entsteht durch lineare Kombination. Eine Schwingung kann als lineare Kombination von Moden hergestellt werden.

Schwingung ohne Dämpfung

Eine Masse und ein Feder bildet ein Feder-Masse-System, wo die Eigenfrequenz ist:

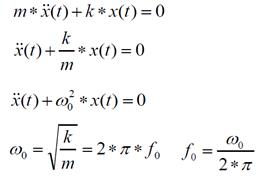
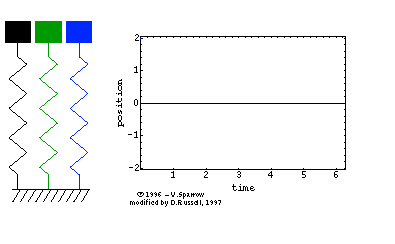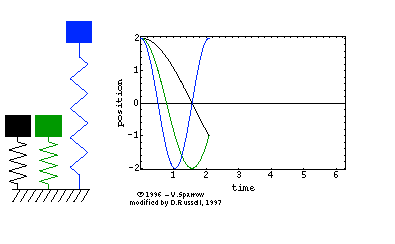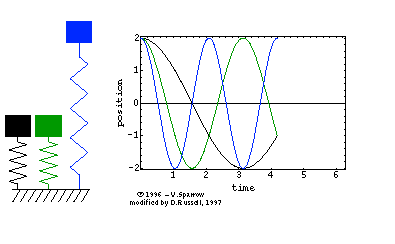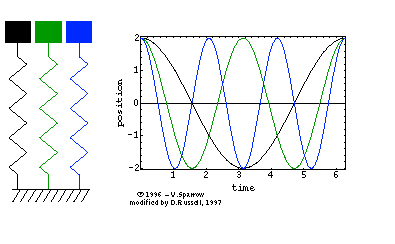
Abbildung. Schwingung ohne Dämpfung.

[http://www.acs.psu.edu/drussell/demos.html]

Ein solches System hat eine Resonanz. Über der Resonanz fällt die Übertragung unter 1. Wenn Dämpfung zu groß ist: kann keine Schwingung entstehen. Wenn Masse grösser wird, die Frequenz fällt.

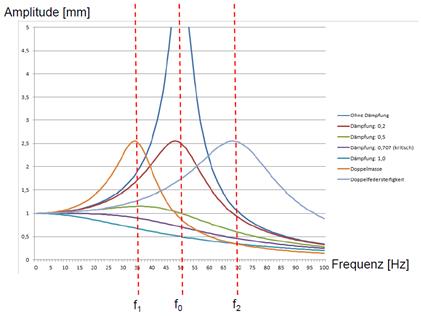
Abbildung. Verschiedene Resonanzkurven.

[http://de.wikipedia.org/wiki/Resonanz]

[https://lp.uni-goettingen.de/get/text/4951]

Schwingung mit Dämpfung (ohne Anregung)

Reale Schwingungen kommen mit Dämpfung vor. Ohne Anregung fällt die Amplitude exponentiell ab. Dämpfung ist mit der Geschwindigkeit proportional

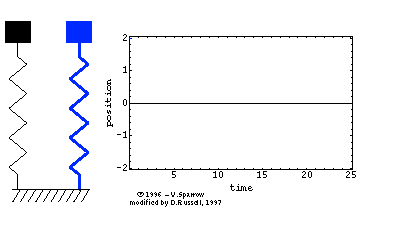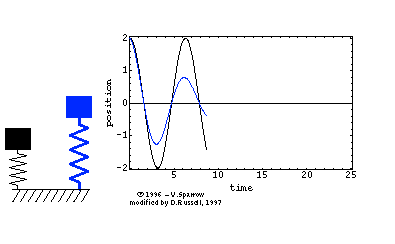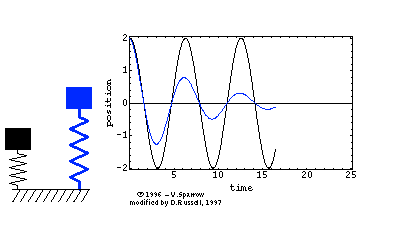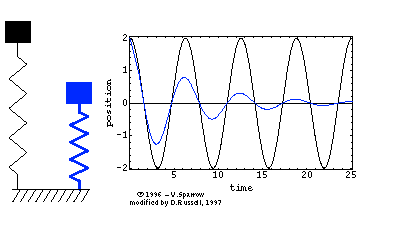
Abbildung. Schwingung mit Dämpfung.

[http://www.acs.psu.edu/drussell/demos.html]

Schwingung mit Dämpfung (mit Anregung)

Die folgende Abbildung zeigt ein reales System mit Dämpfung und Anregung bei 0.4 Hz (unter Resonanz), bei 1 Hz (Resonanz), und bei 1.6 Hz (über Resonanz).

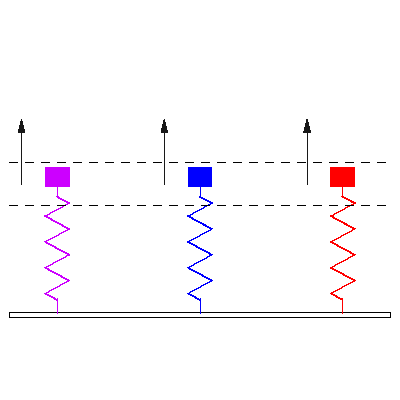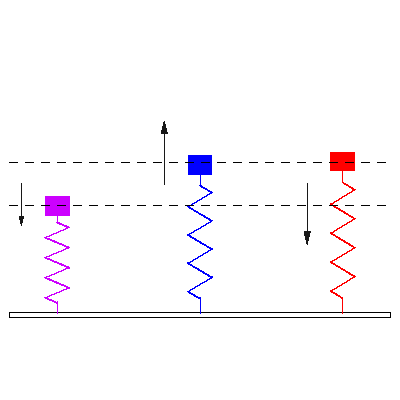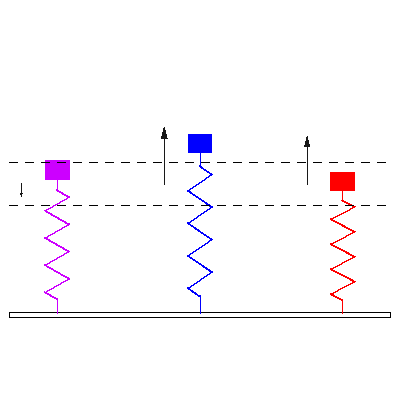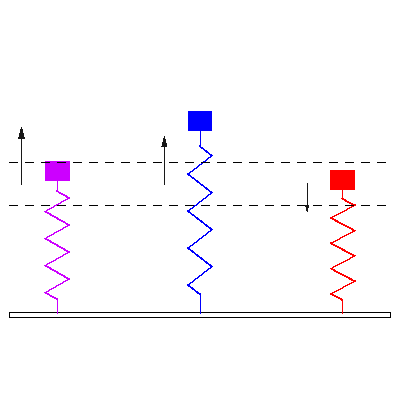
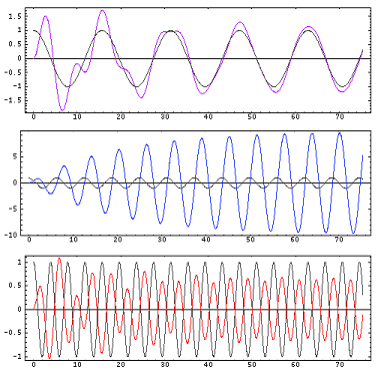
Abbildung. Schwingung mit Dämpfung und Anregung.

[http://www.acs.psu.edu/drussell/demos.html]

10.2 FEM (Finite Element Method)

Die Finite-Elemente-Methode (FEM) ist ein Verfahren zur Lösung von partiellen Differentialgleichungen, wie. z.B. die akustische Wellengleichung. Sie ist ein weit verbreitetes modernes Berechnungsverfahren und ist das Standardwerkzeug bei der Festkörpersimulation. Das Verfahren liefert eine Näherungsfunktion an die exakte Lösung der Differentialgleichung. Zunächst wird das Berechnungsgebiet in eine beliebig große Anzahl von Elementen unterteilt. Diese Elemente sind "endlich" (finit) und nicht unendlich (infinit) klein. Das Aufteilen des Gebiets in eine bestimmte Anzahl Elemente finiter Größe, die sich mit einer endlichen Zahl von Parametern beschreiben lassen, gab der Methode den Namen "Finite-Elemente-Methode". Aus CAD Programmen kann man FE-Modelle von Karosserie, Interieur, Achsen usw. mit Millionen von Elementen herstellen. Eine Analyse ist bis zu mehreren 100 Hz möglich, aber z.B. Fahrgeräusch quantitativ zu prognostizieren ist nicht möglich. Für Körperschall sind modale Gleichungen und die Modalanalyse erforderlich.

Abbildung. FEM eines Motors.

[http://www.ecs.steyr.com/Finite-Elemente-Analyse.3153.0.html

]

10.3 BEM (Boundary Element Method)

Die Randelementmethode (REM, englisch boundary element method, BEM,) ist ein ähnliches Diskretisierungsverfahren zur Berechnung von partiellen Differentialgleichungen und ein numerisches Berechnungsverfahren in den Ingenieurwissenschaften. BEM hat sich etwa parallel mit der Finite-Elemente-Methode (FEM) entwickelt. Bei den meisten Fragestellungen ist jedoch die FEM weiter verbreitet, weil sie weniger Restriktionen bezüglich der Eigenschaften des zu beschreibenden Gebietes aufweist. Bei der Randelementmethode wird, im Gegensatz zur FEM, nur der Rand bzw. die Oberfläche eines Gebietes oder einer Struktur diskretisiert betrachtet, nicht jedoch deren Fläche bzw. Volumen. Die unbekannten Zustandsgrößen befinden sich nur auf dem Rand. Da im Rahmen der Diskretisierung des Problems wird nicht der ganze Betrachtungsraum sondern nur die Oberfläche modelliert, kann das 3D Problem auf ein 2D Problem reduziert werden. http://www.youtube.com/watch?v=6K97dH8AK8o

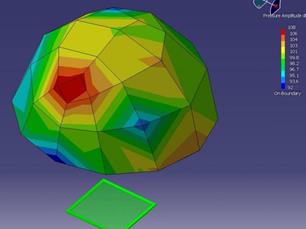
Abbildung. BEM eines Lautsprechers und ein Fahrzeugs.

[http://www.bastra.com/calculation-service/bem/]
[P. Zeller – „Handbuch Fahrzeugakustik“ Vieweg&Teubner Verlag, 2012.]

Problem ist beim FEM, dass es Reflexionen an der Netzgrenze gibt, so werden die Ergebnisse gefälscht. Ein Mikrofon kann nur innerhalb des Netzes sein, und das Netz kann zu groß werden, Man kann auch FEM+BEM zusammen verwenden und das Mikrofon kann innerhalb oder außerhalb sein (PML, AML). Es gibt auch eine iFEM Methode, z.B., unter MATLAB, wo das Netz ist in einer Richtung unendlich ist.

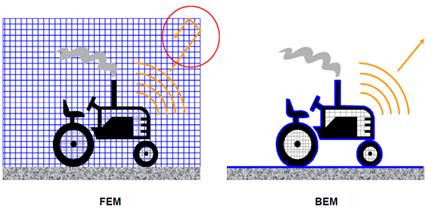
Abbildung. Vergleich FEM und BEM.

[AUDI]

10.4 MKS (Mehrkörpersimulation)

MKS ist eine Methode der numerischen Simulation, bei der reale Mehrkörpersysteme durch mehrere unverformbare Körper abgebildet werden. Es ist für niederfrequente Übertragung gedacht für nichtlineare Schwingungsanalyse im Zeitbereich. Die Bewegungsfähigkeit der Körper zueinander wird durch idealisierte kinematische Gelenke eingeschränkt. Ein Mehrkörpersystem besteht aus Starrkörpern, die durch Gelenke geometrisch, oder durch Feder-Dämpfelemente über Kräfte miteinander gekoppelt sind. Dabei spielt der Schwerpunkt eine wichtige Rolle. MKS Systeme stellen aus dem definierten Modell und den Zwangsbedingungen das Gleichungssystem auf und berechnen das kinematische und dynamische Systemverhalten im Zeitbereich (z.B. Fahrwerkanalyse, Hydrauliksystem) und es können auch nichtlineare Anteile verwendet werden. Die Integration einer FE-Analyse in das MKS-Modell ermöglicht eine Berechnung der Bauteilbelastungen während der Bewegung.

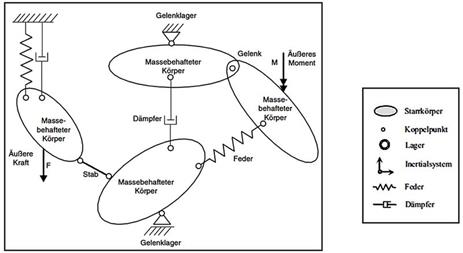
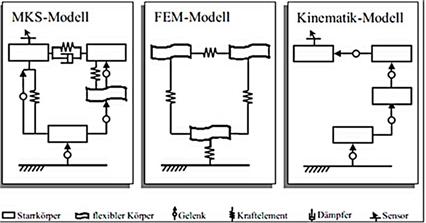
Abbildung. MKS Modell.

[https://wiki.zimt.uni-siegen.de/fertigungsautomatisierung/index.php/Methodiken_zur_Simulationsmodellierung_von_kinematischen_Fertigungsmaschinen_-_Teil_A]

10.5 SEA - Statistische Energieanalyse

Bei räumlich ausgedehnten Strukturen und höheren Frequenzen ist die Annahme starrer Körper nicht mehr zulässig, und so verwendet man FEM. Durch statistische Mittelung über die vielen Eigenschwingformen kann das Problem vereinfacht werden. MKS und FEM Methoden überlappen und sind ca. bis 200 Hz nutzbar, SEA erst über 500 Hz. Es ist geeignet zur Bestimmung der dynamischen Eigenschaften von komplexen, zusammengesetzten Strukturen. Berechnet werden die mittleren Schwingungspegel der einzelnen Teile und der von der Struktur abgestrahlte Schall. Die Behandlung des Schwing- bzw. Körperschallverhaltens und des Schallabstrahlverhaltens ist im modalen Bereich sehr aufwendig oder gar unmöglich. Es entstehen nach aufwendiger Rechnung große Ergebnisdatenmengen, die dann wieder auf die eigentlich gewünschten integralen Größen, wie z.B. mittlerer Schalldruckpegel in der Umgebung der Maschine reduziert werden müssen.

Bei tiefen Frequenzen ist Modendichte klein, und globale Moden können bestimmt werden. Bei hohen Frequenzen ist Modendichte groß, die Moden überlappen so ist SEA anwendbar.

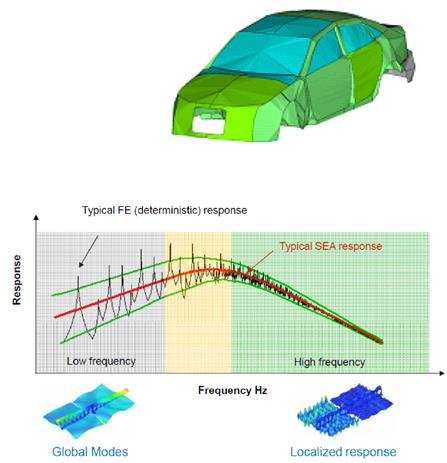
Abbildung. Bei hohen Frequenzen ist Modendichte groß, die Moden überlappen so ist SEA anwendbar.

[AUDI]

Die SEA ist also ein statistisches Berechnungsverfahren, bei dem mit Erwartungswerten der gespeicherten Energien und ausgetauschten Leistungen zwischen gekoppelten Systemen gerechnet wird. Statt exakter Berechnung wird eine gewisse statistische Sicherheit erreicht. Es wird über einen großen Frequenzbereich (Oktav, Terz) gemittelt. In diesem Bereich muss eine Mindestanzahl von Resonanzen liegen (z.B. 6 Moden pro Frequenzband). In der Praxis: nutzbarer Bereich oberhalb 500 Hz.

10.6 PML - Perfectly Matched Layer

PML ist eine numerische Methode für die Simulation der Wellenausbreitung in grenzloser Umgebung (in der Zeitdomäne für FEM). FEM ist generell für interne Probleme benutzt, jetzt kann es für äußere Probleme mit der PML-Schicht ergänzt werden. Das Perfectly Matched Layer (PML) ist eine willkürliche, absorbende Schicht für die Wellengleichung. Die wichtigste Eigenschaft ist: wenn Wellen aus einer nicht-PML Schicht auf die absorbende PML Schicht fällt, werden sie nicht reflektiert. So werden keine Wellen ins Interior reflektiert (welche die Kalkulationen dort einfacher machen können).

Das AML - Automatically Matched Layer ist die automatische Modellierung für die absorbende FEM-Schicht (die PML-Schicht). Es ist das "next generation PML" für Geräuschausstrahlungssimulation. Eine absorbierende Schicht kann simuliert werden (nicht physikalisch durch ein FEM-Netz, sondern es wird auf der Lösungsebene benutzt). Es kann angewendet werden für äußere Strahlung für Motoren oder Kompressoren, für Simulation für Maschinen. Es ist effektiv da weniger Elemente für akustische Probleme nötig seien können (http://www.lmsintl.com/automatically-matched-layer). Die zwei Schritte für äußere Simulation in FEM sind:

Die Lösung wird in der FEM Domäne mit einer PML Schicht bestimmt (Absorption). Wellen breiten in der FEM-Schicht aus, und werden in der PML absorbiert.
Die zweite Berechnung bestimmt den Druck außerhalb der FEM Domäne.

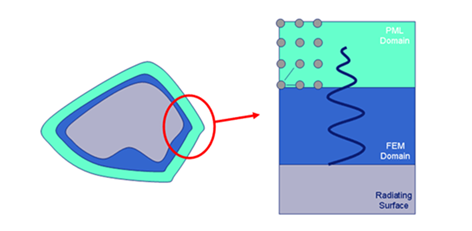
Abbildung. Die Schichten einer strahlenden Struktur. Die abgestrahlten Wellen sind gradweise in der PML-Schicht absorbiert um reflektierten Wellen in der FEM-Domäne zu vermeiden (Freifeld Simulation).

[http://www.engineering.com/DesignSoftware/DesignSoftwareArticles/ArticleID/7230/Actran-for-Acoustic-Radiation-Designs.aspx]

10.7 CFD - Computational Fluid Dynamics

Die numerische Strömungssimulation (CFD) dient in der Produktentwicklung zur Vorhersage der strömungstechnischen Eigenschaften von Bauteilen. Der Einsatz von CFD gestattet es, komplexe Strömungsprobleme in einer frühen Entwicklungsphase zu untersuchen. Simulationen in der Aerodynamik liefern Aussagen über Wechseldrücke auf den Oberflächen und Fluktuationen in der Umströmung, die signifikante akustische Quellen sein können. Im Automobilbau für Fahrzeugklimatisierung, Motorkühlung, Fahrzeug-Umströmung, Fahrzeug-Durchströmung anwendbar. Es können die strömungstechnischen Eigenschaften von Fluiden, also Gas und Flüssigkeiten unter Randbedingungen ermittelt werden. Ergebnisse der CFD Strömungssimulation sind z.B.: Geschwindigkeiten, Strömungsprofile, Druck und Druckverläufe usw. (http://www.youtube.com/watch?v=OeCVFYMcS0E, http://www.youtube.com/watch?v=LXw5OvIP9zM).

10.8 TMM - Transfer-Matrix Method

Das TMM kann anwendbar sein, wenn das ganze System als eine Kette von Subsystemen repräsentiert werden kann (Netz von Subsystemen). Diese Subsysteme sind nur mit den benachbarten Subsystemen in Verbindung. Die Subsysteme sind mit einander durch die Transfer-Matrices geknüpft. Die Matrices können analytisch, experimentell oder numerisch hergestellt werden (COMSOL Modul).

10.9 Raytracing

Raytracing (Strahlverfolgung) ist ein auf der Aussendung von Strahlen basierender Algorithmus zur Verdeckungsberechnung (Sichtbarkeit von Objekten von einem bestimmten Punkt im Raum aus in Optik) und allgemein die Berechnung den weiteren Weg von Strahlen (Wellen) nach dem Auftreffen auf Oberflächen. Strahlen repräsentieren dabei die Normalenvektoren zu einer Wellenfront. Das Ziel ist es, für bestimmte Frequenzen den Energieanteil zu berechnen, der von einem Sender zu einem Empfänger über die verschiedenen möglichen Wege durch die Szene übertragen wird. Zur akustischen Simulation müssen die Materialeigenschaften der verschiedenen Körper sowie die Dämpfung des Schalls durch die Luft berücksichtigt werden. Nachteile sind:

Langsamkeit, da viele Strahlen nie den Empfänger erreichen und für präzise Statistiken eine hohe Anzahl erforderlich ist.
Die Wellenlänge gegenüber den Abmessungen der Körper innerhalb einer Szene ist nicht vernachlässigbar.
Die Beugung von Strahlen kann nicht berücksichtigt werden und zu Fehlern kommen.
http://www.youtube.com/watch?v=aBs0gKThcyM

Abbildung. Raytracing im Auto und in einem Raum.

[http://www.gearslutz.com/board/attachments/studio-building-acoustics/260680d1320071200-isd-gap-my-room-help-pls-chris-nicks-control-room-ray-trace.jpg]

10.10 Ordnungsanalyse

Die Ordnungsanalyse ist Analyse des Geräusches und/oder der Schwingungen von rotierenden Maschinen. Der Energiegehalt des Geräusches wird nicht über der Frequenz sondern über der Ordnung aufgetragen. Das Spektrum wird auf Basis der aktuellen Drehzahl in ein Ordnungsspektrum umgerechnet. Die Ordnung ist dabei ein Vielfaches der Drehzahl. Die Ordnungsanalyse wird entweder bei einer festen, konstanten Drehzahl durchgeführt oder für einen ganzen Hochlauf, bei dem die Maschine von der niedrigsten bis zur höchsten Drehzahl beschleunigt wird. Eine solche Analyse wird auch Signaturanalyse genannt.

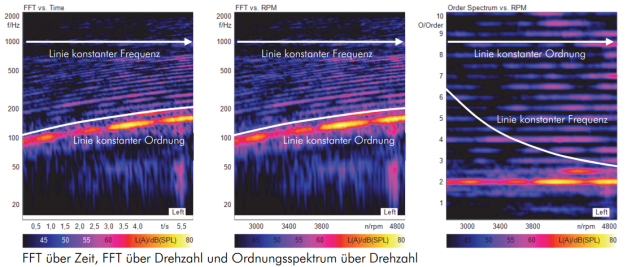
Abbildung. Ordnungsanalyse.

[http://www.head-acoustics.de/downloads/de/application_notes/Ordnungsanalyse_d.pdf]

Bestimmte, je nach Drehwinkel erzeugte Schallemissionen wiederholen sich nach jeder Umdrehung: periodischen Schwingungen in ihrer Frequenz mit der Umdrehungsfrequenz des Motors (bzw. deren Vielfachen) übereinstimmen. Frequenzen, die der Motordrehzahl oder deren Vielfachen entsprechen, sind die Ordnungen. Die 1. Ordnung ist die Frequenz der Motordrehzahl. Die 2. Ordnung ist 1.Ordnung * 2 usw.

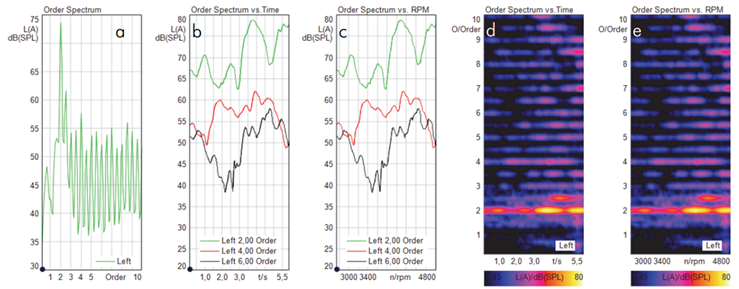
Abbildung. Verschiedene Varianten der Ordnungsanalyse: Bei der Analyse wird der Pegel(verlauf) dieser Ordnungen berechnet z.B. gemittelt (a), über der Zeit (b und d), über der Drehzahl (c und e).

[http://www.head-acoustics.de/downloads/de/application_notes/Ordnungsanalyse_d.pdf]

10.11 Lineare und nicht lineare Analyse

Lineare Analyse hat die folgenden wichtigsten Eigenschaften:

Kleine Störungen, Perturbationen
Medium ist linear
Analyse im Frequenzbereich
Beispiele: FEM, BEM, SEA

Nicht lineare Analyse hat die folgenden wichtigsten Eigenschaften:

Große Störungen, Veränderungen
Medium ist nicht linear
Analyse im Zeitbereich (FFT, wenn periodisch)
Beispiele: MKS, CFD

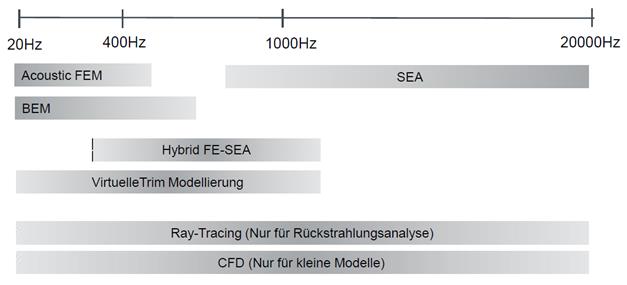
Abbildung. Zusammenfassung von numerischen Methoden.

[AUDI]

*********************************************************************************************************************

11. Quellen

P. Zeller (Hsg): Handbuch Fahrzeugakustik: Grundlagen, Auslegung, Berechnung, Versuch (ATZ/MTZ-Fachbuch) [Gebundene Ausgabe], Verlag: Vieweg+Teubner Verlag; Auflage: 2., überarb. Aufl. 2012 (16. Dezember 2011), Sprache: Deutsch, ISBN-10: 3834814431, ISBN-13: 978-3834814432
LotharCremer, Michael Möser, ManfredHeckl, Wolfgang Kropp: Körperschall: Physikalische Grundlagen und technische Anwendungen [Gebundene Ausgabe], Gebundene Ausgabe: 580 Seiten, Verlag: Springer; Auflage: 3., aktualisierte Aufl. 2010 (30. Oktober 2009), Sprache: Deutsch, ISBN-10: 3540403361, ISBN-13: 978-3540403364
Michael Möser: Technische Akustik [Gebundene Ausgabe], Gebundene Ausgabe: 560 Seiten, Verlag: Springer; Auflage: 9., aktualisierte Aufl. 2012 (27. September 2012), Sprache: Deutsch, ISBN-10: 3642309321, ISBN-13: 978-3642309328
F. Alton Everest , Ken C. Pohlmann: Master Handbook of Acoustics [Englisch] [Taschenbuch], Taschenbuch: 528 Seiten, Verlag: Mcgraw-Hill Publ.Comp.; Auflage: 5th edition. (1. Juli 2009), Sprache: Englisch, ISBN-10: 0071603328, ISBN-13: 978-0071603324
Jens Blauert: Communication Acoustics [Englisch] [Taschenbuch], Taschenbuch: 396 Seiten, Verlag: Springer Berlin Heidelberg; Auflage: Softcover reprint of hardcover 1st ed. 2005 (27. April 2010), Sprache: Englisch, ISBN-10: 3642060609, ISBN-13: 978-3642060601
Hermann Henn: Ingenieurakustik: Physikalische Grundlagen und Anwendungsbeispiele (German Edition) [Taschenbuch], Taschenbuch: 472 Seiten, Verlag: Vieweg+Teubner Verlag; Auflage: 4., überarb. u. erw. Aufl. 2008 (28. August 2008), Sprache: Deutsch, ISBN-10: 3834802557, ISBN-13: 978-3834802552
Ian Stewart: Welt-Formeln, rororo Verlag, ISBN 978-3-499-63029-3
Youtube
Dan Russell: http://www.acs.psu.edu/drussell/demos.html
Wikipedia
HeadAcoustics homepage and tutorials
Bang and Olufsen homepage
AudiTV
Audi